
【题目】如图,![]() 是
是![]() 的弦,
的弦,![]() 为半径
为半径![]() 的中点,过
的中点,过![]() 作
作![]() 交弦于点
交弦于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() 、
、![]() ,求
,求![]() 的度数:
的度数:
(3)如果![]() ,
,![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)证明见解析; (2)30°;(3)![]() .
.
【解析】
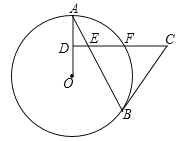
(1)连接OB,由圆的半径相等和已知条件证明∠OBC=90°,即可证明BC是⊙O的切线;
(2)连接OF,AF,BF,首先证明△OAF是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数;
(3)作CG⊥BE于G,如图,利用等腰三角形的性质得BG=5,再证明∠OAB=∠ECG,则sin∠ECG=sin∠OAB=![]() ,于是可计算出CE=13,从而得到DE=2,由
,于是可计算出CE=13,从而得到DE=2,由![]() ,得
,得![]() ,
, ![]() ,即可求出
,即可求出![]() 的半径.
的半径.
![]() 连接
连接![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线;
的切线;
(2)连接OF,AF,BF,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]()
![]() .
.
(3)过点![]() 作
作![]() 于
于![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
∴![]() ,
,
在![]() 中,
中,
![]() ,sin∠ECG=sin∠OAB=
,sin∠ECG=sin∠OAB=![]() ,
,
![]() ,
,![]() ,
,
又![]()
![]() ,
,
![]() .
.
由![]() ,得:
,得:![]() ,
,
![]()
![]() ,
,
![]() 的半径为
的半径为![]() .
.



 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
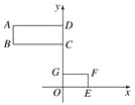
【题目】如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(-4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为( )
A. (0,3)
B. (0,2.5)
C. (0,2)
D. (0,1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
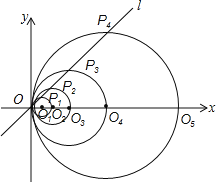
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B(0,2),A(﹣6,﹣1)在反比例函数![]() 的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数
的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数![]() 图象于点C,则点C的坐标为_____.
图象于点C,则点C的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,点C是弧AB的中点,点D是弧BC的中点,连接AC,BC,AD,BD,且AD与BC相交于点F,延长AC至E,使AC=EC,连接EB交AD的延长线于点G.
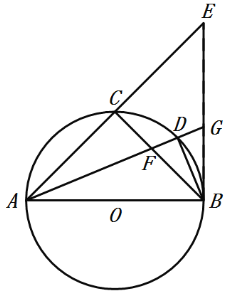
(1)求证:EB是⊙O的切线;
(2)求证;AF=2BD;
(3)求证:线段BG是线段CF和线段EG的比例中项.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA· PB=PC·PD
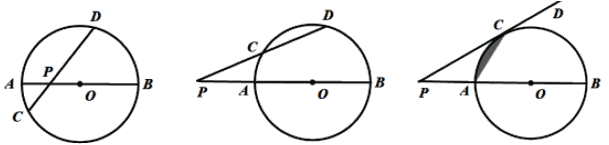
(1)如图(2),若AB与CD相交于圆外一点P, 上面的结论是否成立?请说明理由.
(2)如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系.
(3)如图(3),直接利用(2)的结论,求当 PC= ![]() ,PA=1时,阴影部分的面积.
,PA=1时,阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中进行“选科走班”教学改革,语文、数学、英语三门为必修学科,另外还需从物理、化学、生物、政治、历史、地理(分别记为A、B、C、D、E、F)六门选修学科中任选三门,现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.
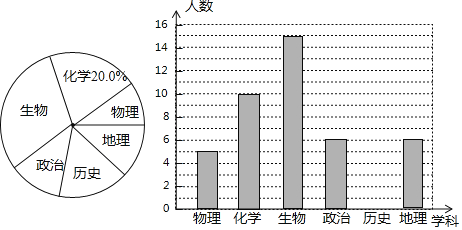
请根据以上信息,完成下列问题:
(1)该班共有学生人;
(2)请将条形统计图补充完整;
(3)该班某同学物理成绩特别优异,已经从选修学科中选定物理,还需从余下选修学科中任意选择两门,请用列表或画树状图的方法,求出该同学恰好选中化学、历史两科的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧AB的中点,弦CD与AB相交于E.
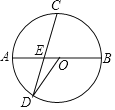
(1)若∠AOD=45°,求证:CE=![]() ED;(2)若AE=EO,求tan∠AOD的值.
ED;(2)若AE=EO,求tan∠AOD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 是线段
是线段![]() 的垂直平分线,交线段
的垂直平分线,交线段![]() 于点
于点![]() ,在
,在![]() 下方的直线
下方的直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,以线段
,以线段![]() 为边,在
为边,在![]() 上方作正方形
上方作正方形![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
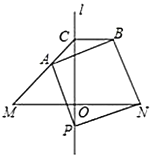
(1)设![]() ,求
,求![]() 的度数;
的度数;
(2)写出线段![]() 、
、![]() 之间的等量关系,并证明.
之间的等量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com