
【题目】如图,在![]() 中,∠A=90°,
中,∠A=90°,![]() 是
是![]() 的中点,过点
的中点,过点![]() 的直线
的直线![]() 、
、![]() 交直线
交直线![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,连接
,连接![]() .
.
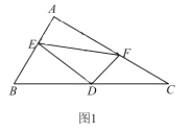
(1)如图1,求证:![]() ;
;
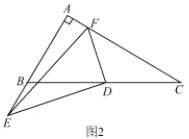
(2)如图2,若![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长度.(不必写过程)
的长度.(不必写过程)
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)如图1中,延长ED到H,使得ED=DH,连接FH,CH.想办法证明EF=FH,CH=BE,∠FCH=90°即可解决问题;
(2)如图2中,延长ED到H,使得ED=DH,连接FH,CH.作DK⊥AC于K.,设AC交DH于点O.想办法求出CH的长,利用(1)中结论即可解决问题;
解:(1)如图1中,延长ED到H,使得ED=DH,连接FH,CH.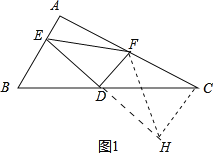
∵BD=DC,DE=DH,∠BDE=∠CDH,
∴△BDE≌△CDH(SAS),
∴BE=CH,∠B=∠DCH,
∵∠A=90°,
∴∠ACB+∠B=∠ACB+∠DCH=90°,
∴∠FCH=90°,
∴FH2=FC2+CH2=FC2+BE2,
∵FD⊥EH,DE=DH,
∴EF=FH,
∴EF2=BE2+CF2;
(2)如图2中,延长ED到H,使得ED=DH,连接FH,CH.作DK⊥AC于K.,设AC交DH于点O.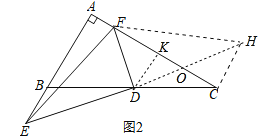
同(1)的方法易证△BDE≌△CDH(SAS),∠FCH=90°,DK∥CH,
∴BE=CH,可得EF2=BE2+CF2,
∵∠A=90°,AB=6,∠ACB=30°,
∴BC=12
∴AC= ![]() ,
,
∵AF=![]() ,
,
∴CF=5![]() ,
,
∵BD=DC,DK∥AB,
∴AK=KC=3![]() ,FK=2
,FK=2![]() ,DK=
,DK=![]() AB=3,
AB=3,
∴DF=![]() ,
,
∵OD⊥DF,DK⊥OF,
∴![]() ,
,![]() ,
,
∴OK=![]() ,
,
∴OC=![]() =
=![]() ,
,
∴OC= OK,
∵DK∥CH,
∴∠ODK=∠OHC,∠OKD=∠OCH,
∴△OHC≌△ODK,
∴CH= DK =3,
∴EF=![]() ,
,


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
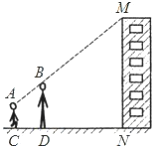
【题目】亮亮和颖颖两人用下面方法测量楼高:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距CD=1.25m,颖颖与楼之间的距离DN=30m(C,D,N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m.求住宅楼的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P1.P2是反比例函数y=![]() (k>0)在第一象限图象上的两点,点A1的坐标为(2,0),若△P1OA1与△P2A1A2均为等边三角形.
(k>0)在第一象限图象上的两点,点A1的坐标为(2,0),若△P1OA1与△P2A1A2均为等边三角形.
(1)求此反比例函数的解析式;
(2)求A2点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 上取点
上取点![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ;在
;在![]() 上取一点
上取一点![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ;…,按此做法进行下去,第n个等腰三角形的底角
;…,按此做法进行下去,第n个等腰三角形的底角![]() 的度数为__________.
的度数为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,![]() 的顶点均在格点上,建立平面直角坐标系后,点
的顶点均在格点上,建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
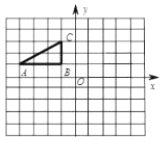
(1)先将![]() 向右平移5个单位,再向下平移1个单位后得到
向右平移5个单位,再向下平移1个单位后得到![]() ,试在图中画出图形
,试在图中画出图形![]() ;
;
(2)将![]() 绕点
绕点![]() 顺时针旋转90°后得到
顺时针旋转90°后得到![]() ,试在图中画出图形
,试在图中画出图形![]() ,并计算
,并计算![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当![]() 时,求1千瓦时的电量汽车能行驶的路程;
时,求1千瓦时的电量汽车能行驶的路程;
(2)当![]() 时求
时求![]() 关于
关于![]() 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com