
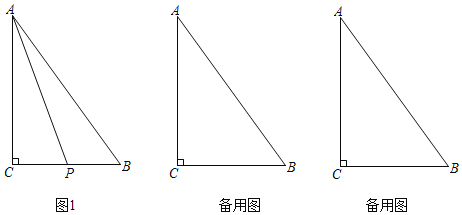
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.
(1)若点![]() 恰好在
恰好在![]() 的角平分线上,求
的角平分线上,求![]() 的值;
的值;
(2)若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
【答案】(1)![]() 或6;(2)
或6;(2)![]() 或5或
或5或![]() 或
或![]() .
.
【解析】
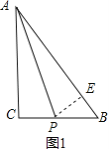
(1)当点P在∠CAB的平分线上时,如图1,过点P作PE⊥AB于点E,此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,根据勾股定理列方程即可得到结论;
(2)在Rt△ABC中,根据勾股定理得到AC=4cm,根据题意得:AP=2t,当P在AC上时,△BCP为等腰三角形,得到PC=BC,即4-2t=3,求得t=![]() ,当P在AB上时,△BCP为等腰三角形,若CP=PB,点P在BC的垂直平分线上,如图2,过P作PE⊥BC于E,求得t=
,当P在AB上时,△BCP为等腰三角形,若CP=PB,点P在BC的垂直平分线上,如图2,过P作PE⊥BC于E,求得t=![]() ,若PB=BC,即2t-3-4=3,解得t=5,③PC=BC,如图3,过C作CF⊥AB于F,由射影定理得;BC2=BFAB,列方程32=
,若PB=BC,即2t-3-4=3,解得t=5,③PC=BC,如图3,过C作CF⊥AB于F,由射影定理得;BC2=BFAB,列方程32=![]() ,即可得到结论.
,即可得到结论.
解:(1)当点![]() 在
在![]() 的平分线上时,如图1,过点
的平分线上时,如图1,过点![]() 作
作![]() 于点
于点![]() ,
,
此时![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
解得:![]() ,
,
当![]() 时,点
时,点![]() 与
与![]() 重合,也符合条件,
重合,也符合条件,
![]() 当
当![]() 或6时,
或6时,![]() 在
在![]() 的角平分线上;
的角平分线上;
(2)在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
根据题意得:![]() ,
,
当![]() 在
在![]() 上时,
上时,![]() 为等腰三角形,
为等腰三角形,
![]() ,即
,即![]() ,
,
![]() ,
,
当![]() 在
在![]() 上时,
上时,![]() 为等腰三角形,
为等腰三角形,
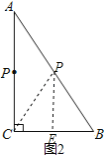
①![]() ,点
,点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
如图2,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
②![]() ,即
,即![]() ,
,
解得:![]() ,
,
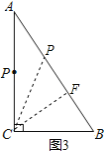
③![]() ,如图3,过
,如图3,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
由射影定理得:![]() ,
,
即![]() ,
,
解得:![]() ,
,
综上:若![]() 为等腰三角形,t的值为
为等腰三角形,t的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=50m,BC=40m,∠C=90°,边AC,BC上有两动点P,Q,点P从点A开始沿边AC向点C以2m/s的速度匀速移动,同时另一点Q由点C开始以3m/s的速度沿着边CB向点B匀速移动,当一动点到达终点时,另一点也随之停止移动.几秒后,△PCQ的面积等于450m2

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠A=90°,
中,∠A=90°,![]() 是
是![]() 的中点,过点
的中点,过点![]() 的直线
的直线![]() 、
、![]() 交直线
交直线![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,连接
,连接![]() .
.
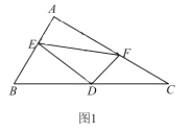
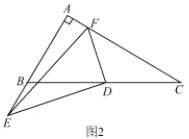
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长度.(不必写过程)
的长度.(不必写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() ,射线
,射线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() .
.
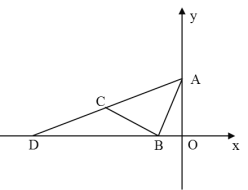
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 是坐标平面内不同于点
是坐标平面内不同于点![]() 的一点,且以
的一点,且以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标;
的坐标;
(3)点![]() 是线段
是线段![]() 上一点,直线
上一点,直线![]() 交
交![]() 于点
于点![]() ,且
,且![]() 的面积等于
的面积等于![]() 面积的一半,求点
面积的一半,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() .
.
(1)如图1,点![]() 、
、![]() 都在
都在![]() 外部,连接
外部,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 与
与![]() 相交于
相交于![]() 点,判断
点,判断![]() 与
与![]() 的关系,说明理由,若
的关系,说明理由,若![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 的外部,连接
的外部,连接![]() 、
、![]() 、
、![]() 、
、![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
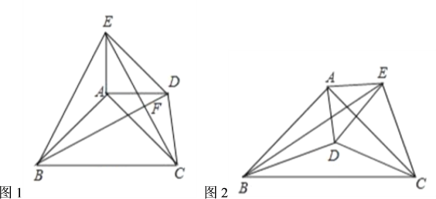
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.

(1)求![]() 的度数:
的度数:
(2)如图2,连接![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解用电紧张,龙泉县电力公司特制定了新的用电收费标准:每月用电量x(千瓦时)与应付电费y(元)的关系如图所示.
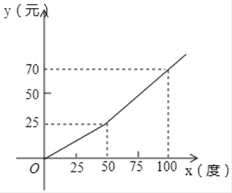
(1)根据图象求出y与x之间的函数关系式;
(2)当用电量超过50千瓦时时,收费标准是怎样的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+2x与直线y= ![]() 交于A,B两点,与直线x=2交于点P,将抛物线沿着射线AB平移
交于A,B两点,与直线x=2交于点P,将抛物线沿着射线AB平移![]() 个单位.
个单位.

(1)平移后的抛物线顶点坐标为_______;
(2)在整个平移过程中,点P经过的路程为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com