
【题目】今年3月12日植树节,美华中学为了进一步绿化学校,计划购买甲、乙两种树苗共计50棵.设购买甲种树苗![]() 棵,有关甲、乙两种树苗的信息如下:甲种树苗每棵50元,乙种树苗每棵80元;甲种树苗的成活率为90%,乙种树苗的成活率为95%.
棵,有关甲、乙两种树苗的信息如下:甲种树苗每棵50元,乙种树苗每棵80元;甲种树苗的成活率为90%,乙种树苗的成活率为95%.
(1)根据信息填表(用含![]() 的式子表示):
的式子表示):
树苗类型 | 甲种树苗 | 乙种树苗 |
购买树苗的数量(单位:棵) |
| |
购买树苗的费用(单位:元) |
(2)如果购买甲、乙两种树苗共用去2560元,那么甲、乙两种树苗各购买了多少棵?
(3)如果要使这批树苗的成活率不低于92%,请设计一种购买甲、乙树苗的方案,使购买甲、乙两种树苗的费用最少,写出购买方案并计算出购买甲、乙两种树苗的总费用.
【答案】(1)见解析;(2)甲种树苗购买了48棵,乙种树苗购买了2棵;(3)购买方案为购买甲树30棵,乙树20棵.购买甲、乙两种树苗的总费用为3100元.
【解析】
(1)根据两种树苗共购买50棵,再结合题目中的单价即可填表;
(2)根据(1)中表格信息以及共花费2560元即可列出方程,求解即可;
(3)根据这批树苗的成活率不低于92%列出不等式求解即可.
解:(1)根据信息填表
树苗类型 | 甲种树苗 | 乙种树苗 |
购买树苗的数量(单位:棵) |
|
|
购买树苗的费用(单位:元) |
|
|
(2)由(1)可得:![]()
解得![]() ,
,
答:甲种树苗购买了48棵,乙种树苗购买了2棵;
(3)由题意,得![]()
解得![]()
由题意得:购买甲树越多,乙树越少,则总费用越少;
购买方案:购买甲树30棵,乙树20棵;
![]() (元)
(元)
答:购买方案为购买甲树30棵,乙树20棵.购买甲、乙两种树苗的总费用为3100元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了治理大气污染,我国西部某市抽取了该市2019年中120天的空气质量指数,绘制了如下不完整的统计图表:

(1) ![]() ;
;![]() .
.
(2)请把空气质量指数的条形统计图补充完整;
(3)若绘制“空气质量指数的扇形统计图”,级别为“优”所对应扇形的圆心角的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
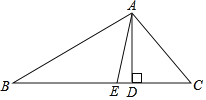
【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
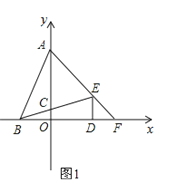
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
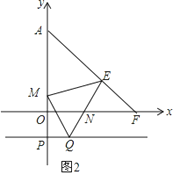
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架云梯长25 m,斜靠在一面墙上,梯子靠墙的一端距地面24 m.
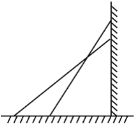
(1)这个梯子底端离墙有多少米?
(2) 如果梯子的顶端下滑了4m,那么梯子的底部在水平方向也滑动了4m吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
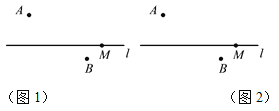
【题目】作图题:已知点A,点B,直线l及l上一点M.
(1)如图1,连接MA,并在直线l上作出一点N,使得点N在点M的左边,且满足MN=MA,作线段MN的中点C,连接BC;
(2)如图2,请在直线l上确定一点O,使点O到点A与点O到点B的距离之和最短,并写出画图的依据.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com