
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
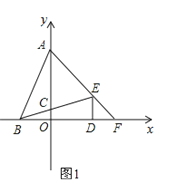
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
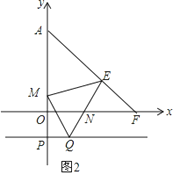
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
【答案】(1)A(0,3) B(-1,0) D(2,0);(2)![]() E(2,1) F(3,0);(3)
E(2,1) F(3,0);(3)![]()
【解析】
(1)由非负数的性质可求得a、b、d的值,可求得A、B、D的坐标;
(2)由条件可证明△ABO≌△BED,可求得DE和BD的长,可求得E点坐标,再求得直线AE与BE的解析式,可求得C、F点坐标;
(3)过E作EG⊥OA于点G,EH⊥PQ于点Q,可证明四边形GEHP为正方形,在GA上截GI=QH,可证明△IGE≌△QHE,可证得∠IEM=∠MEQ=45°,可证明△EIM≌△EQM,可得到IM=MQ,再结合条件可求得PH=AI=PQ,可求得答案.
解:(1)∵![]() ,
,
∴![]()
∴![]() ,
,
∴A(0,3),B(-1,0),D(2,0);
(2)∵A(0,3),B(-1,0),D(2,0),
∴OB=1,OD=2,OA=3,
∴AO=BD,
在△ABO和△BED中,
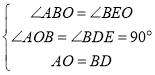 ,
,
∴△ABO≌△BED(AAS),
∴DE=BO=1,
∴E(2,1),
设直线AE解析式为:y=kx+b,直线BE解析式为:y=mx+n,如图1,
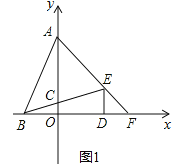
把点A、E代入y=kx+b,把点B、E代入y=mx+n,得
![]() ,
,![]() ,
,
解得:![]() ,
, ,
,
∴直线AE解析式为:![]() ,
,
直线BE解析式为:![]() ,
,
∴直线![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
∴点F为:![]() ,
,
∴直线![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
∴点C为:![]() ;
;
(3)过E作EG⊥OA,EH⊥PQ,垂足分别为G、H,在GA上截取GI=QH,如图2,

∵E(2,1),P(-1,0),
∴GE=GP=GE=PH=2,
∴四边形GEHP为正方形,
∴∠IGE=∠EHQ=90°,
在Rt△IGE和Rt△QHE中
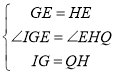 ,
,
∴△IGE≌△QHE(SAS),
∴IE=EQ,∠1=∠2,
∵∠QEM=45°,
∴∠2+∠3=45°,
∴∠1+∠3=45°,
∴∠IEM=∠QEM,
在△EIM和△EQM中,
 ,
,
∴△EIM=EQM(SAS),
∴IM=MQ,
∴AM-MQ=AM-IM=AI,
由(2)可知OA=OF=3,∠AOF=90°,
∴∠A=∠AEG=45°,
∴PH=GE=GA=IG+AI,
∴AI=GA-IG=PH-QH=PQ,
![]()


科目:初中数学 来源: 题型:
【题目】已知,点P是直角三角形ABC斜边AB上一点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.

(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,若AC=BC,CE:AE=1:3,△FBQ的面积等于3,求△AQE的面积;
(3)如图3,当点P在线段BA的延长线上时,请画出符合条件的图形.若AC=BC,AE:CE=1:3,△FEQ的面积等于3,求△AQE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠BAC=∠EAD=90o.
(1)判断∠BAE与∠CAD的大小关系,并说明理由.
(2)当∠EAC=60o时,求∠BAD的大小.
(3)探究∠EAC与∠BAD的数量关系,请直接写出结果,不要求说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)
①b>0
②a﹣b+c<0
③阴影部分的面积为4
④若c=﹣1,则b2=4a.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月12日植树节,美华中学为了进一步绿化学校,计划购买甲、乙两种树苗共计50棵.设购买甲种树苗![]() 棵,有关甲、乙两种树苗的信息如下:甲种树苗每棵50元,乙种树苗每棵80元;甲种树苗的成活率为90%,乙种树苗的成活率为95%.
棵,有关甲、乙两种树苗的信息如下:甲种树苗每棵50元,乙种树苗每棵80元;甲种树苗的成活率为90%,乙种树苗的成活率为95%.
(1)根据信息填表(用含![]() 的式子表示):
的式子表示):
树苗类型 | 甲种树苗 | 乙种树苗 |
购买树苗的数量(单位:棵) |
| |
购买树苗的费用(单位:元) |
(2)如果购买甲、乙两种树苗共用去2560元,那么甲、乙两种树苗各购买了多少棵?
(3)如果要使这批树苗的成活率不低于92%,请设计一种购买甲、乙树苗的方案,使购买甲、乙两种树苗的费用最少,写出购买方案并计算出购买甲、乙两种树苗的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△ADE,线段BC的延长线过点E,与线段AD交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B=48°,则∠DEF的度数_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
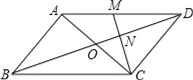
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
(1)如图1,若AB=12,BD=![]() BC,求线段CD的长度;
BC,求线段CD的长度;
![]()
(2)如图2,点E是线段AB上一点,且AE=2BE,当3AD=2BD时,探究线段CD与CE之间的数量关系,请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com