【题目】如图，△ABC≌△ADE，线段BC的延长线过点E，与线段AD交于点F，∠ACB＝∠AED＝108°，∠CAD＝12°，∠B＝48°，则∠DEF的度数_____．
【答案】36°
【解析】
由△ACB的内角和定理求得∠CAB＝24°；然后由全等三角形的对应角相等得到∠EAD＝∠CAB＝24°．则结合已知条件易求∠EAB的度数；最后利用△AEB的内角和是180度和图形来求∠DEF的度数．
解：∵∠ACB＝108°，∠B＝48°，
∴∠CAB＝180°﹣∠B﹣∠ACB＝180°﹣48°﹣108°＝24°．
又∵△ABC≌△ADE，
∴∠EAD＝∠CAB＝24°．
又∵∠EAB＝∠EAD+∠CAD+∠CAB，∠CAD＝12°，
∴∠EAB＝24°+12°+24°＝60°，
∴∠AEB＝180°﹣∠EAB﹣∠B＝180°﹣60°﹣48°＝72°，
∴∠DEF＝∠AED﹣∠AEB＝108°﹣72°＝36°．
故答案为：36°
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，数轴的单位长度为1．
（1）如果点A，D表示的数互为相反数，那么点B表示的数是多少？
（2）如果点B，D表示的数互为相反数，那么图中表示的四个点中，哪一点表示的数的绝对值最大？为什么？
（3）当点B为原点时，若存在一点M到A的距离是点M到D的距离的2倍，则点M所表示的数是____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．
（1）求这个二次函数的解析式；
（2）是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；
（3）动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A（0，b）、点B（a，0）、点D（d，0）且a、b、c满足
．DE⊥x轴且∠BED=∠ABD，BE交y轴于点C，AE交x轴于点F．
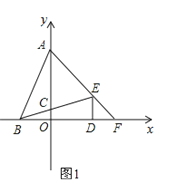
（1）求点A、B、D的坐标；
（2）求点C、E、F的坐标；
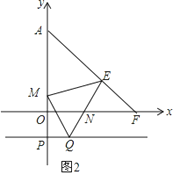
（3）如图，过P（0，-1）作x轴的平行线，在该平行线上有一点Q（点Q在P的右侧）使∠QEM=45°，QE交x轴于N，ME交y轴正半轴于M，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，中线BE，CD相交于点O，连接DE，下列结论：①
＝
；②
＝；③
＝
；④
＝
.其中正确的个数为( )
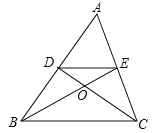
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一架云梯长25 m，斜靠在一面墙上，梯子靠墙的一端距地面24 m.
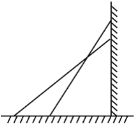
(1)这个梯子底端离墙有多少米？
(2) 如果梯子的顶端下滑了4m，那么梯子的底部在水平方向也滑动了4m吗?为什么?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点D为OB上的一点，按下列要求进行尺规作图（保留作图痕迹），并回答问题．
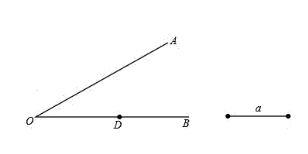
（1）作∠AOB的平分线OC，在OC上取一点P使得OP＝a；
（2）过点P作OA边上的高；
（3）在边OA上取一点E，使得PE＝PD，请写出∠OEP与∠ODP的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
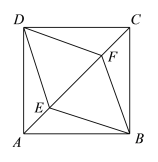
【题目】如图，E，F是正方形ABCD的对角线AC上的两点，且AE＝CF.
(1)求证：四边形BEDF是菱形；
(2)若正方形ABCD的边长为4，AE＝
，求菱形BEDF的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
