
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x与一次函数y=﹣x+7的图象交于点A,x轴上有一点P(a,0).
x与一次函数y=﹣x+7的图象交于点A,x轴上有一点P(a,0).
(1)求点A的坐标;
(2)若△OAP为等腰三角形,则a= ;
(3)过点P作x轴的垂线(垂线位于点A的右侧)、分别交y=![]() x和y=﹣x+7的图象于点B、C,连接OC.若BC=
x和y=﹣x+7的图象于点B、C,连接OC.若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

【答案】(1)A(4,3);(2)±5或8或![]() ;(3)28
;(3)28
【解析】
(1)点A是两直线的交点,其坐标即方程组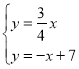 的解;
的解;
(2)分OA=PO、OA=AP、AP=OP适中情况,分别求解即可;
(3)P(a,0),则分别用含a的式子表示出B、C的坐标,从而表示出BC的长度,用勾股定理求得OA,然后根据BC=![]() OA求出a的值,从而利用三角形面积公式求解.
OA求出a的值,从而利用三角形面积公式求解.
解:(1)由题意: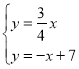 解得:
解得:![]() ,
,
故点A(4,3);
(2)点A(4,3),则OA=![]() ,
,
①当OA=PO=P1O时,
此时OA=5=PO=P1O,即a=±5

②当OA=AP时,如图,过点A做AM⊥x轴于点M
此时OM=MP=4
∴OP=8
则点P(8,0),即a=8;
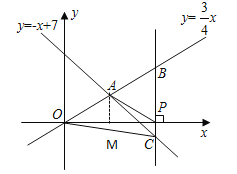
③当AP=OP时,如图所示,连接AP,过点A作AH⊥x轴于点H,
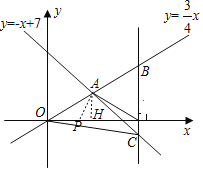
AP=PO=a,则PH=4﹣a,则(4﹣a)2+9=a2,
解得:a=![]() ;
;
综上,a=±5或8或![]() ;
;
故答案为:±5或8或![]() ;
;
(3)∵P(a,0),则点B、C的坐标分别为:(a,![]() a)、(a,﹣a+7),
a)、(a,﹣a+7),
∴BC=![]() a-(-a+7)=
a-(-a+7)=![]() a+a﹣7=
a+a﹣7=![]()
又∵BC=![]() OA且OA=
OA且OA=![]()
∴![]() =
=![]() ×5=7,
×5=7,
解得:a=8,
故点P(8,0),即OP=8;
△OBC的面积=![]() ×BC×OP=
×BC×OP=![]() ×7×8=28.
×7×8=28.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
(1)求抛物线的函数解析式;
(2)若D是抛物线位于第一象限上的动点,求△BCD面积的最大值及此时点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
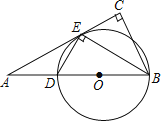
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
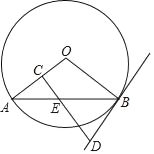
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
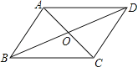
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:常用的分解因式方法有提公因式、公式法等,但有的多项式只有上述方法就无法分解,如x2﹣4y2+2x﹣4y,细心观察这个式子会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:
x2﹣4y2+2x﹣4y
=(x2﹣4y2)+(2x﹣4y)
=(x+2y)(x﹣2y)+2(x﹣2y)
=(x﹣2y)(x+2y+2)
这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:x2﹣6xy+9y2﹣3x+9y
(2)△ABC的三边a,b,c满足a2﹣b2﹣ac+bc=0,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与证明:
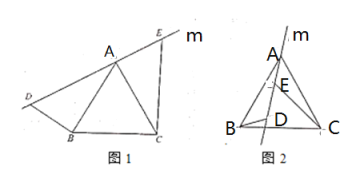
(1)如图1,直线![]() 经过正三角形
经过正三角形![]() 的项点
的项点![]() ,在直线
,在直线![]() 上取两点
上取两点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并子以证明:
之间满足的数量关系,并子以证明:
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图2的位置,并使
逆时针方向旋转一个角度到如图2的位置,并使![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com