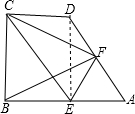
(1)证明:连接DE,
∵E为AB的中点,
∴AB=2AE=2BE,
∵AB=2DC,
∴CD=BE,
∵CD∥AB,∠CBA=90°,
∴四边形CBED是矩形,
∵F为AD中点,∠DEA=90°,
∴EF=AF,
∵∠A=60°,
∴△AEF是正三角形,
∴AE=EF=AF,∠EFA=60°,
∵AE=BE,DF=AF
∴BE=EF=AF,CD=DF,
∴∠CFE=90°=∠CBE,
∵CD∥AB,
∴∠CDF=180°-∠A=120°,
∴∠DFC=30°,
∴∠CFE=90°=∠CBE,
∵在Rt△CBE和Rt△CFE中
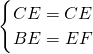
∴Rt△CBE≌Rt△CFE(HL);
(2)解:∵CD=a,
∴AE=BE=a,
∵∠A=60°,
∴
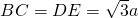
,
∴
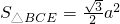
,
∴S
四边形BCFE=2S
△BCE=

a
2.
分析:连接DE,求出CD=BE,得出矩形BEDC,推出∠DEB=90°,根据直角三角形斜边上中线性质得出FE=AF,得出等边三角形EFA,求出EF=AE=BE,∠EFA=60°,求出∠DFC=30°,求出∠CFE=90°,根据HL证出粮三角形全等即可;
(2)根据勾股定理求出DE,BC,求出△CBE面积,即可求出答案.
点评:本题考查了梯形性质,矩形的性质和判定,等边三角形的性质和判定,平行线的性质,三角形的内角和定理,等腰三角形的性质,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理的能力,题目综合性比较强,难度偏大.

 在直角梯形ABCD中,AB∥CD,∠ABC=90°,∠A=60°,AB=2CD,E,F分别为AB,AD的中点,连结EF,EC,BF,CF.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,∠A=60°,AB=2CD,E,F分别为AB,AD的中点,连结EF,EC,BF,CF. (1)证明:连接DE,
(1)证明:连接DE,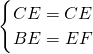
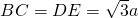 ,
,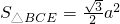 ,
, a2.
a2.

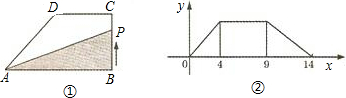
 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为