
【题目】如图,已知一次函数y=mx+n的图像与x轴交于点B,与反比例函数![]() (k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(1)若OA=11,求k的值;
(2)沿着x轴向右平移直线BC,若直线经过H点时恰好又经过点D,求一次函数函数y=mx+n的表达式.

【答案】(1)k=18;(2)![]() .
.
【解析】
(1)由∠HCB=∠HCA及CH⊥x轴得到△CHB≌△CHA,推出BH=HA=8,由BC=6根据勾股定理求出CH,由OA=11进而得出C点坐标,求得k值;
(2)过D点作DN⊥x轴于N点,由H是AB中点且HD∥BC得到D是AC的中点,设C点坐标,进而表示出D点坐标,根据k相等即可建立方程求解.
解:(1)∵CH⊥x轴
∴∠CHB=∠CHA=90°
在△CHB和△CHA中
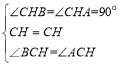 ,∴△CHB≌△CHA(ASA)
,∴△CHB≌△CHA(ASA)
∴BH=AH=![]() AB=8
AB=8
在△BCH中,由勾股定理可知:![]()
且OH=OA-AH=11-8=3
故C点的坐标为:(3,6)
∴反比例的k=3×6=18.
故答案为:18.
(2) 过D点作DN⊥x轴于N点,如下图所示:
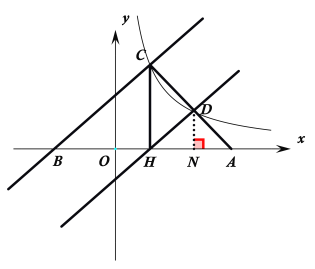
设C点坐标为(a,6),∴OH=a,CH=6
由HD∥BC,且H是AB的中点可知
HD是△ABC的中位线,且D是AC的中点
又DN⊥CH,∴DN∥CH
∴DN是△ACH的中位线
∴DN=![]() CH=4,HN=NA=
CH=4,HN=NA=![]() AH=4
AH=4
∴ON=OH+HN=a+4
∴D点的坐标为(a+4,3)
又∵C、D均在反比例函数上,
∴6×a=(a+4)×3
解之得:a=4,故C点坐标为(4,6)
BO=BH-OH=8-4=4,故B点坐标为(-4,0)
将C(4,6)和B(-4,0)代入y=mx+n中:
![]() ,解之得:
,解之得:![]()
故一次函数的解析式为:![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有理数范围内,我们定义三个数之间的新运算“![]() ”法则:a
”法则:a![]() b
b![]() c=|a+b+c|-a+b-c,例如:1
c=|a+b+c|-a+b-c,例如:1![]() 2
2![]() (-3)=|1+2+(-3)|-1+2-(-3)=4.在
(-3)=|1+2+(-3)|-1+2-(-3)=4.在![]() 这6个数中,任意取三个数作为a、b、c的值,则a
这6个数中,任意取三个数作为a、b、c的值,则a![]() b
b![]() c的最大值为___________
c的最大值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,点E是边AB上一动点(不与A,B重合),延长BA至点F,使AF=BE,连接CE,DF.
(1) 判断四边形CEFD的形状,并说明理由;
(2) 如图①,连接AC,过点E作EH⊥AC,垂足为点H.
①证明:AH=EH;
②若BE:AE=1:![]() ,求∠BCE的度数;
,求∠BCE的度数;
③如图②,连接FH,在点E的运动过程中,![]() 的值是否发生变化?若不变,求出
的值是否发生变化?若不变,求出![]() 的值;若变化,请说明理由.
的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3600名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.

(1)参与本次问卷调查的学生共有 人,其中选择D类的人数有 人;
(2)在扇形统计图中,求E类对应的扇形圆心角![]() 的度数,并补全C对应的条形统计图;
的度数,并补全C对应的条形统计图;
(3)若将A、B、C.D.E这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点.
的图象相交于A、B两点.

(1)根据图象,分别写出A、B的坐标;
(2)求出两函数解析式;
(3)根据图象回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值.
为何值时,一次函数的函数值大于反比例函数的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为
点对应的数为![]() ,
,![]() 点对应的数为
点对应的数为![]() .
.
![]()
(1)请写出与![]() 、
、![]() 两点距离相等的点
两点距离相等的点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚁![]() 从
从![]() 点出发,以
点出发,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?(写出计算过程)
点对应的数是多少吗?(写出计算过程)
(3)在题(2)中,若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
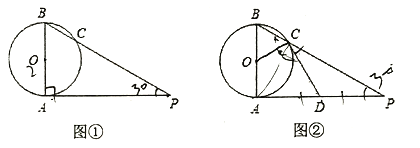
【题目】己知AB是⊙0的直径,AP是⊙0的切线,A是切点,BP与⊙0交于点C.
(1)如图①,若AB=2,∠P=30![]() ,求AP的长.(结果保留根号)
,求AP的长.(结果保留根号)
(2)如图②,若D为AP的中点,∠P=30![]() ,求证:直线CD是⊙O的切线.
,求证:直线CD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com