
【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为
点对应的数为![]() ,
,![]() 点对应的数为
点对应的数为![]() .
.
![]()
(1)请写出与![]() 、
、![]() 两点距离相等的点
两点距离相等的点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚁![]() 从
从![]() 点出发,以
点出发,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?(写出计算过程)
点对应的数是多少吗?(写出计算过程)
(3)在题(2)中,若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
【答案】(1)40;(2)28;(3)11秒或13秒.
【解析】
(1)由题意可知,点M是AB的中点,根据数轴上中点距离公式求解即可;
(2)求出相遇时所用的时间,然后计算即可;
(3)分相遇前和相遇后两种情况,根据时间=路程÷总速度分别列式计算即可.
解:(1)由题意可知点M是AB的中点,
∴点M所对应的数为:![]() ;
;
(2)相遇时所用的时间为:[100-(-20)]÷(4+6)=12秒,
∴![]() 点对应的数为:-20+12×4=28;
点对应的数为:-20+12×4=28;
(3)由题意可得:A,B之间的距离为120,运动时间为t秒,两只蚂蚁的距离为10,
分情况讨论:
①相遇前,两只蚂蚁的距离为10,则t=(120-10)÷(4+6)=11秒,
②相遇后,两只蚂蚁的距离为10,则t=(120+10)÷(4+6)=13秒,
∴运动11秒或13秒时,两只蚂蚁的距离为10


科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B分别表示数a、b,且|a+6|+|b-10|=0,记AB=|a-b|
(1) 求AB的值
(2) 如图,点P、Q分别从点A、B出发沿数轴向右运动,点P的速度是每秒4个单位长度,点Q的速度是每秒1个单位长度,点C从原点出发沿数轴向右运动,速度是每秒3个单位长度.经过多少秒,点C与点P、Q的距离相等?
![]()
(3) 在(2)的条件下,点M从对应-8的点出发沿数轴向左运动,速度是每秒4个单位长度,在运动过程中,MP+MC-3MQ的值是否为定值?若是,求出其值,若不是,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=mx+n的图像与x轴交于点B,与反比例函数![]() (k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(1)若OA=11,求k的值;
(2)沿着x轴向右平移直线BC,若直线经过H点时恰好又经过点D,求一次函数函数y=mx+n的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图都是由7个小立方体搭成的几何体,从不同方向看几何体,分别画出它们的主视图、左视图与俯视图,并在小正方形内填上表示该位置的小正方体的个数.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:
1,﹣![]() ,8.9,﹣7,
,8.9,﹣7, ![]() ,﹣3.2,+1 008,﹣0.06,28,﹣9.
,﹣3.2,+1 008,﹣0.06,28,﹣9.
正整数集合:{______…};
负整数集合:{______…};
正分数集合:{______…};
负分数集合:{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
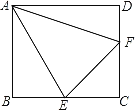
【题目】如图,正方形ABCD中,点E、F分别在边BC、CD上,连接AE、EF、AF,且∠EAF=45°,下列结论:
①△ABE≌△ADF;
②∠AEB=∠AEF;
③正方形ABCD的周长=2△CEF的周长;
④S△ABE+S△ADF=S△CEF,其中正确的是_____.(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=![]() 的图像经过B、C两点.
的图像经过B、C两点.

(1)求该二次函数的解析式;
(2)结合函数的图像探索:当y>0时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com