
【题目】如图,正方形ABCD中,点E、F分别在边BC、CD上,连接AE、EF、AF,且∠EAF=45°,下列结论:
①△ABE≌△ADF;
②∠AEB=∠AEF;
③正方形ABCD的周长=2△CEF的周长;
④S△ABE+S△ADF=S△CEF,其中正确的是_____.(只填写序号)
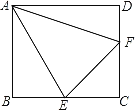
【答案】②③
【解析】
当E、F不是BC和CD的中点时,BE≠DF,则△ABE和△ADF的边对应不相等,由此判断①;延长CD至G,使得DG=BE,证明△ABE≌△ADG和△AEF≌△AGF,即可判断②;通过周长公式计算,再由BE+DF=EF,即可判断③;证明S△ABE+S△ADF=S△AGF,再由三角形的底与高的数量关系得S△AGF>S△CEF,进而判断④.
解:①当E、F不是BC和CD的中点时,BE≠DF,则△ABE≌△ADF不成立,故①错误;
②延长CD至G,使得DG=BE,连接AG,如图1,
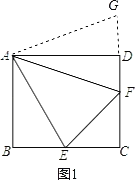
∵四边形ABCD为正方形
∴AB=AD,∠ABE=∠ADG=90°,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,∠AEB=∠G,AE=AG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠GAF=∠DAG+∠DAF=45°,
∴∠EAF=∠GAF,
∵AF=AF,
∴△AEF≌△AGF(SAS),
∴∠AEF=∠G,
∴∠AEB=∠AEF,故②正确;
③∵△AEF≌△AGF,
∴EF=GF=DG+DF=BE+DF,
∴△CEF的周长=CE+CF+EF=CE+CF+BE+DF=BC+CD=2BC,
∵正方形ABCD的周长=4BC,
∴正方形ABCD的周长=2△CEF的周长,故③正确;
④∵△ABE≌△ADG,
∴S△ABE=S△ADG,
∴S△ABE+S△ADF=S△AGF,
∵GF=EF>CF,AD≥CE,
∴![]() ,即S△AGF>S△CEF,
,即S△AGF>S△CEF,
∴S△ABE+S△ADF≠S△CEF,故④错误;
故答案为:②③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
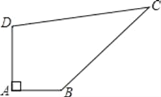
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3600名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.

(1)参与本次问卷调查的学生共有 人,其中选择D类的人数有 人;
(2)在扇形统计图中,求E类对应的扇形圆心角![]() 的度数,并补全C对应的条形统计图;
的度数,并补全C对应的条形统计图;
(3)若将A、B、C.D.E这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为
点对应的数为![]() ,
,![]() 点对应的数为
点对应的数为![]() .
.
![]()
(1)请写出与![]() 、
、![]() 两点距离相等的点
两点距离相等的点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚁![]() 从
从![]() 点出发,以
点出发,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?(写出计算过程)
点对应的数是多少吗?(写出计算过程)
(3)在题(2)中,若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东走了3千米到达小彬家,继续向东走了2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家、小彬家、小颖家的位置;
(2)小明家离小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.08升,这次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
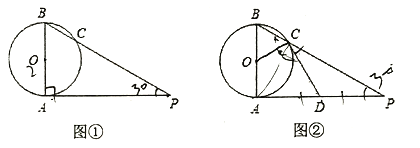
【题目】己知AB是⊙0的直径,AP是⊙0的切线,A是切点,BP与⊙0交于点C.
(1)如图①,若AB=2,∠P=30![]() ,求AP的长.(结果保留根号)
,求AP的长.(结果保留根号)
(2)如图②,若D为AP的中点,∠P=30![]() ,求证:直线CD是⊙O的切线.
,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
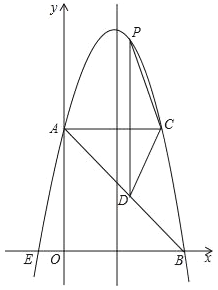
【题目】如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红富士苹果某箱上标明苹果质量为![]() ,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”)
,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com