
 如图,△AOB中,∠AOB=120°,BD,AC是两条高,连接CD,若AB=4,则DC的长为( )
如图,△AOB中,∠AOB=120°,BD,AC是两条高,连接CD,若AB=4,则DC的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{4}$ |
分析 由△MAC∽△MBD推出△MDC∽△MBA得$\frac{DC}{AB}=\frac{MD}{MB}$=$\frac{1}{2}$即可解决问题.
解答  解:如图延长AD、BC交于点M.
解:如图延长AD、BC交于点M.
∵∠AOB=120°,
∴∠DOA=∠COB=60°,
∵AD⊥BD,AC⊥BC,
∴∠ADM=∠MDB=∠ACB=∠ACM=90°,
∴∠MAC=∠MBD=30°,
∴△MAC∽△MBD,
∴$\frac{MA}{MB}=\frac{MC}{MD}$,
∴$\frac{MA}{MC}=\frac{MB}{MD}$,∠M=∠M,
∴△MDC∽△MBA,
∴$\frac{DC}{AB}=\frac{MD}{MB}$,
在RT△MBD中,∵∠MBD=30°,
∴MB=2MD,
∵AB=4,
∴$\frac{DC}{4}=\frac{1}{2}$,
∴DC=2.
故选B.
点评 本题考查相似三角形的判定和性质、直角三角形中30度角的性质,添加辅助线构造相似三角形是解决问题的关键.


科目:初中数学 来源: 题型:选择题
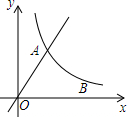 如图,直线y=$\frac{3}{4}$x与双曲线y=$\frac{k}{x}$(x>0)交于点A,将直线y=$\frac{3}{4}$x向右平移6个单位后,与双曲线y=$\frac{k}{x}$(x>0)交于点B,与x轴交于点C,若A点到x轴的距离是B点到x轴的距离的2倍,那么k的值为( )
如图,直线y=$\frac{3}{4}$x与双曲线y=$\frac{k}{x}$(x>0)交于点A,将直线y=$\frac{3}{4}$x向右平移6个单位后,与双曲线y=$\frac{k}{x}$(x>0)交于点B,与x轴交于点C,若A点到x轴的距离是B点到x轴的距离的2倍,那么k的值为( )| A. | 7$\sqrt{2}$ | B. | 12 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
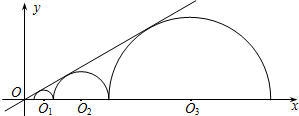 如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016=32015.
如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016=32015.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 总收入(单位:万元) | 总支出(单位:万元) | 利润(单位:万元) | |
| 去年 | x | y | 200 |
| 今年 | 1.2x | 0.9y | 780 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com