

���� ��1������S=S��ABO-S��EOD���ɽ����
��2���������ADF������RT��������DF=$\sqrt{3}$AD�г����̿������t�����������E��G�������ֱ��BG�������M���ɽ����
��3�����P��m��-$\frac{\sqrt{3}}{4}$m2+$\frac{3\sqrt{3}}{4}$��������PQ�е�C��$\frac{m+\sqrt{3}}{2}$��-$\frac{\sqrt{3}}{8}$m2+$\frac{3\sqrt{3}}{8}$�������ֱ��RC����m��ʾ�߶�PK��HN������PK=HN�г����̽ⷽ�̼��ɣ�
��� �⣺��1����ֱ��y=-$\sqrt{3}$x+$\sqrt{3}$��x�ύ��A��1��0������y�ύ��B��0��$\sqrt{3}$����
��S=S��ABO-S��EOD=$\frac{1}{2}$��$1��\sqrt{3}$-$\frac{1}{2}$��$��1-t����\sqrt{3}-\sqrt{3}t��$=$\frac{\sqrt{3}}{2}$t2-$\sqrt{3}$t��0��t��1����
��2����tan��BAO=$\frac{OB}{OA}$=$\sqrt{3}$M
���BAO=60�㣬
�ߡ�FDA=90�㣬
��DF��OE��EF��OD��
���ı���EFDO��ƽ���ı��Σ�
�ߡ�EOD=90�㣬
���ı���EFDO�Ǿ��Σ�
��DF=EO=$\sqrt{3}$AD��
��$\sqrt{3}$-$\sqrt{3}$t=$\sqrt{3}$t
��t=$\frac{1}{2}$��
���E��0��$\frac{\sqrt{3}}{2}$����G��2��$\frac{\sqrt{3}}{2}$����
��ֱ��BGΪy+kx+b����$\left\{\begin{array}{l}{b=\sqrt{3}}\\{2k+b=\frac{\sqrt{3}}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{4}}\\{b=\sqrt{3}}\end{array}\right.$��
��ֱ��BGΪ��y=-$\frac{\sqrt{3}}{4}$x+$\sqrt{3}$��
�ඥ��M��1��$\frac{3\sqrt{3}}{4}$����
��������Ϊ��y=a��x-1��2+$\frac{3\sqrt{3}}{4}$���ѵ�E�����a=-$\frac{\sqrt{3}}{4}$��
����������y=-$\frac{\sqrt{3}}{4}$��x-1��2+$\frac{3\sqrt{3}}{4}$��
��3����ͼ3�У���������������Ϊ��y=-$\frac{\sqrt{3}}{4}$x2+$\frac{3\sqrt{3}}{4}$��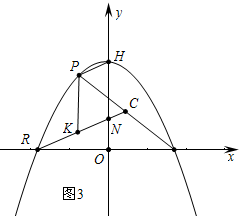
��y=0�õ�x=$��\sqrt{3}$��
��R��-$\sqrt{3}$��0����Q��$\sqrt{3}$��0����H��0��$\frac{3\sqrt{3}}{4}$����
��P��m��-$\frac{\sqrt{3}}{4}$m2+$\frac{3\sqrt{3}}{4}$��������PQ�е�C��$\frac{m+\sqrt{3}}{2}$��-$\frac{\sqrt{3}}{8}$m2+$\frac{3\sqrt{3}}{8}$����
��ֱ��RCΪy=kx+b����$\left\{\begin{array}{l}{-\sqrt{3}k+b=0}\\{\frac{m+\sqrt{3}}{2}k+b=-\frac{\sqrt{3}}{8}{m}^{2}+\frac{3\sqrt{3}}{8}}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}��{m}^{2}-3��}{4��m+3\sqrt{3}��}}\\{b=-\frac{3��{m}^{2}-3��}{4��m+3\sqrt{3}��}}\end{array}\right.$��
��ֱ��RCΪ��y=-$\frac{\sqrt{3}��{m}^{2}-3��}{4��m+3\sqrt{3}��}$x-$\frac{3��{m}^{2}-3��}{4��m+3\sqrt{3}��}$��
���K��m��-$\frac{\sqrt{3}m��{m}^{2}-3��}{4��m+3\sqrt{3}��}$-$\frac{3��{m}^{2}-3��}{4��m+3\sqrt{3}��}$
���ı���PKNH��ƽ���ı��Σ�
��PK=HN��
��-$\frac{\sqrt{3}}{4}{m}^{2}+\frac{3\sqrt{3}}{4}$+$\frac{\sqrt{3}m��{m}^{2}-3��}{4��m+3\sqrt{3}��}$+$\frac{3��{m}^{2}-3��}{4��m+3\sqrt{3}��}$=$\frac{3\sqrt{3}}{4}$+$\frac{3��{m}^{2}-3��}{4��m+3\sqrt{3}��}$��
�����õ���$\frac{\sqrt{3}}{4}$m2=$\frac{\sqrt{3}m��{m}^{2}-3��}{4��m+3\sqrt{3}��}$��m=-$\frac{\sqrt{3}}{3}$����0��������
���P���꣨-$\frac{\sqrt{3}}{3}$��$\frac{2\sqrt{3}}{3}$����
���� ���⿼����κ�����һ�κ������й������Լ����������������ǵ����Ǻ�����ƽ���ı��ε��ж������ʵ�֪ʶ������������÷��̵�˼���ǽ������Ĺؼ���


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
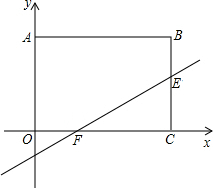 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�������ABCO�ı�OA��OC�ֱ���y�ᡢx���ϣ�OA=3��OC=4��ֱ��y=$\frac{2}{3}$x-$\frac{2}{3}$�볤����ABCO�ı�OC��BC�ֱ���F��E�����CEF������ǣ�������
��ͼ��ʾ����ƽ��ֱ������ϵ�У�������ABCO�ı�OA��OC�ֱ���y�ᡢx���ϣ�OA=3��OC=4��ֱ��y=$\frac{2}{3}$x-$\frac{2}{3}$�볤����ABCO�ı�OC��BC�ֱ���F��E�����CEF������ǣ�������| A�� | 6 | B�� | 3 | C�� | 12 | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{9}$ | B�� | $\sqrt{18}$ | C�� | $\sqrt{12}$ | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=-1���䲿��ͼ����ͼ��ʾ����֪ax2+bx+c=0���������ֱ�Ϊx1��x2����x1��x2����x2��ȡֵ��Χ��0��x2��1��
������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=-1���䲿��ͼ����ͼ��ʾ����֪ax2+bx+c=0���������ֱ�Ϊx1��x2����x1��x2����x2��ȡֵ��Χ��0��x2��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
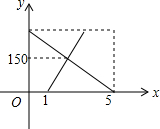 һ��������A�س�����һ�����ٶ�����ʻ��B�أ�1Сʱ��һ��С������B�س�����ͬһ��·����ʻ��A�أ����С�����Ȼ�����1Сʱ�ﵽĿ�ĵأ�������B�صľ���y��km��������ʱ��x��h���ĺ�����ϵ��ͼ��ʾ����С��������1.5Сʱ�������������
һ��������A�س�����һ�����ٶ�����ʻ��B�أ�1Сʱ��һ��С������B�س�����ͬһ��·����ʻ��A�أ����С�����Ȼ�����1Сʱ�ﵽĿ�ĵأ�������B�صľ���y��km��������ʱ��x��h���ĺ�����ϵ��ͼ��ʾ����С��������1.5Сʱ��������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����AOB�У���AOB=120�㣬BD��AC�������ߣ�����CD����AB=4����DC�ij�Ϊ��������
��ͼ����AOB�У���AOB=120�㣬BD��AC�������ߣ�����CD����AB=4����DC�ij�Ϊ��������| A�� | $\sqrt{3}$ | B�� | 2 | C�� | $\frac{3\sqrt{3}}{2}$ | D�� | $\frac{3\sqrt{3}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬BD��CE���ڵ�O��������������������
��ͼ���ڡ�ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬BD��CE���ڵ�O���������������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com