练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．已知S1=x，S2=3S1-2，S3=3S2-2，S4=3S3-2，…，S2015=3S2014-2，则S2015=32014x-32014+1．（结果用含x的代数式表示）．

    分析 根据已知，分别计算出S1、S2、S3、S4，观察结果可以看出结果的一次项系数和常数项都是3的幂的关系式，进而得出答案．

    解答 解：根据已知得：
    S1=x，
    S2=3S1-2=3x-2
    S3=3S2-2=9x-8，
    S4=3S3-2=27x-26，
    S5=3S4-2=81x-80，
    观察以上等式：
    3=31，9=32，27=33，81=34，
    ∴S2015=32014x-（32014-1）=32014x-32014+1．
    故答案为：32014x-32014+1．

    点评 此题目考查了数字的变化规律，通过等式的变形，总结出其中的规律，利用计算规律解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．在平面直角坐标系中，已知点O为坐标原点，直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别相交于A、B两点，动点D、E分别从A、B两点同时出发，沿坐标轴向终点O运动．过点E作x轴的平行线与直线AB相交于点F，点D、E的运动速度分别是每秒1个单位长度、每秒$\sqrt{3}$个单位长度，它们的运动时间为t秒．
    （1）如图1，连接DE，设四边形ADEF的面积为S，求出S与t之间的函数关系式，并直接写出自变量t的取值范围；
    （2）如图2，抛物线y=a（x-k）2+h（a＜0）经过点E，与直线EF相交于另一点G，它的对称轴l经过点A，顶点为M，连接BG、DF，当∠ADF=90°，且顶点M恰好落在BG上时，求这条抛物线的解析式；
    （3）如图3，将（2）中的抛物线向左平移1个单位长度，得到一条新的抛物线，此抛物线与x轴相交于点R，Q（R在Q的左侧），与y轴相交于点H，在第二象限内新抛物线上有一个动点P，连接PQ、PH、点C为线段PQ的中点，连接CR，与y轴相交于点N．过点P作y轴的平行线与CR相交于点K，当四边形PKNH是平行四边形时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．小知识：古希腊的毕达哥拉斯，在2500年前曾经大胆断言，一条线段（AB）的某一部分（AC）与另一部分（BC）之比，如果正好等于另一部分（BC）同整个线段（AB）的比（即BC2=AC．AB），那么这样的比例会给人一种美感，后来我们将分割这条线段（AB）的点C称为线段AB的“黄金分割点”，
    在主持节目时，主持人站在舞台的黄金分割点处最自然得体，那么在长20米的舞台AB上，主持人从A点到B点走多少米，他的站台最得体？（取$\sqrt{2}$=1.4，$\sqrt{3}$=1.7，$\sqrt{5}$=2.2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在下列式子中：1，2x2y，$\frac{a+b}{2}$，$\frac{3+y}{x}$，$\frac{1}{b}$，a+1，$\frac{x+y}{10}$，整式共有（　　）
    A．5个B．6个C．7个D．8个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

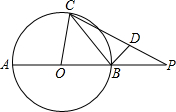    6．如图，AB是⊙O的直径，延长AB至P，使BP=OB，BD垂直于弦BC，垂足为点B，点D在PC上．设∠PCB=α，∠POC=2β．求证：tanα•tanβ=$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．在直角坐标系中，点A（2，1）向下平移2个单位长度后的坐标为（　　）
    A．（4，1）B．（0，1）C．（2，3）D．（2，-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．若单项式x2y3与$\frac{1}{2}$x2yb是同类项，则b的值为3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，已知直线y=-$\frac{3}{4}$x+3分别交x轴、y轴于点A、B，P是抛物线y=-$\frac{1}{2}$x2+2x+5上的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=-$\frac{3}{4}$x+3于点Q，则当PQ=BQ时，a的值是4+2$\sqrt{5}$或4-2$\sqrt{5}$或4或-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算题
    （1）5.6+（-0.9）+4.4+（-8.1）+（-0.1）
    （2）-0.5+（-3$\frac{1}{4}$）+（-2.75）+（+7$\frac{1}{2}$）
    （3）1$\frac{2}{3}$+（-1$\frac{2}{5}$）+$\frac{4}{3}$+（-1）+（-3$\frac{3}{5}$）
    （4）$\frac{1}{2}$+（-$\frac{2}{3}$）+（-$\frac{4}{5}$）+（-$\frac{1}{2}$）+（-$\frac{1}{3}$）
    （5）（-0.8）+1.2+（-0.7）+（-2.1）+0.8+3.5
    （6）（-1$\frac{3}{4}$）+（-6$\frac{1}{3}$）+（-2.25）+$\frac{10}{3}$．

    查看答案和解析>>

    同步练习册答案