
 小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一部分(AC)与另一部分(BC)之比,如果正好等于另一部分(BC)同整个线段(AB)的比(即BC2=AC.AB),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”,
小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一部分(AC)与另一部分(BC)之比,如果正好等于另一部分(BC)同整个线段(AB)的比(即BC2=AC.AB),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”,科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{18}$ | C. | $\sqrt{12}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:
如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
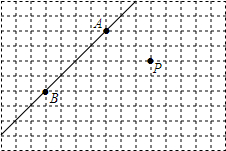 在如图所示的方格纸上,只用直尺画图.
在如图所示的方格纸上,只用直尺画图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一般地,y=$\frac{k}{x+a}$与y=$\frac{k}{x}$的图象的形状、大小均完全相同,把函数y=$\frac{k}{x}$的图象进行适当的平移就可以得到y=$\frac{k}{x+a}$的图象.已知y=$\frac{1}{x}$与y=$\frac{1}{x-2}$在同一坐标系中的图象如图所示,则不等式$\frac{1}{x-2}>\frac{1}{x}$的解集为( )
一般地,y=$\frac{k}{x+a}$与y=$\frac{k}{x}$的图象的形状、大小均完全相同,把函数y=$\frac{k}{x}$的图象进行适当的平移就可以得到y=$\frac{k}{x+a}$的图象.已知y=$\frac{1}{x}$与y=$\frac{1}{x-2}$在同一坐标系中的图象如图所示,则不等式$\frac{1}{x-2}>\frac{1}{x}$的解集为( )| A. | x>2 | B. | 0<x<2 | C. | x<0或x>2 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com