

���� ��1������ͼ����Ϣ���ɵó����ۣ�
��2�����ֱ��AB��y=$\frac{3}{4}$x-$\frac{3}{2}$����P��a��$\frac{3}{4}$a-$\frac{3}{2}$��������S��POD+S��OAP=$\frac{1}{2}$S�����OABCD�г����̽ⷽ�̼��ɣ�
��� �⣺��1����ͼ���֪A��2��0����B��6��3����
m=$\frac{1}{2}$��4��2=4��
��2����ֱ��ABΪy=kx+b�������⣺$\left\{\begin{array}{l}{2k+b=0}\\{6k+b=3}\end{array}\right.$���$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{3}{2}}\end{array}\right.$��
��ֱ��ABΪy=$\frac{3}{4}$x-$\frac{3}{2}$����P��a��$\frac{3}{4}$a-$\frac{3}{2}$����
��S�����OABCD=4��2+$\frac{1}{2}$��1+4��•4=18��
�����⣺S��POD+S��OAP=9��
��$\frac{1}{2}$��4��a+$\frac{1}{2}$��2����$\frac{3}{4}$a-$\frac{3}{2}$��=9��
��a=$\frac{42}{11}$��
���P��$\frac{42}{11}$��$\frac{15}{11}$����
��ֱ��DPΪy=k��x+4��P�����k��=-$\frac{29}{42}$��
��ֱ��DP�Ľ���ʽΪ��y=-$\frac{29}{42}$x+4��
���� ���⿼��һ�κ������й����ʡ��������������֪ʶ������ͼ����Ϣ��Ŀ������ͼ����Ϣ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
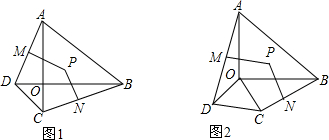
 ��ͼ�����ı���ABCD�У��Խ���AC��BD���ڵ�E��AE=2��CE=3��AB=2��D��AC�ľ���Ϊ1�����ı���ABCD�������
��ͼ�����ı���ABCD�У��Խ���AC��BD���ڵ�E��AE=2��CE=3��AB=2��D��AC�ľ���Ϊ1�����ı���ABCD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С֪ʶ����ϣ���ıϴ����˹����2500��ǰ�������ԣ�һ���߶Σ�AB����ijһ���֣�AC������һ���֣�BC��֮�ȣ�������õ�����һ���֣�BC��ͬ�����߶Σ�AB���ıȣ���BC2=AC��AB������ô�����ı��������һ�����У��������ǽ��ָ������߶Σ�AB���ĵ�C��Ϊ�߶�AB�ġ��ƽ�ָ�㡱��
С֪ʶ����ϣ���ıϴ����˹����2500��ǰ�������ԣ�һ���߶Σ�AB����ijһ���֣�AC������һ���֣�BC��֮�ȣ�������õ�����һ���֣�BC��ͬ�����߶Σ�AB���ıȣ���BC2=AC��AB������ô�����ı��������һ�����У��������ǽ��ָ������߶Σ�AB���ĵ�C��Ϊ�߶�AB�ġ��ƽ�ָ�㡱���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5�� | B�� | 6�� | C�� | 7�� | D�� | 8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ֪��y=-$\frac{3}{4}$x+3�ֱ�x�ᡢy���ڵ�A��B��P��������y=-$\frac{1}{2}$x2+2x+5�ϵ�һ�����㣬�������Ϊa������P��ƽ����y���ֱ�߽�ֱ��y=-$\frac{3}{4}$x+3�ڵ�Q����PQ=BQʱ��a��ֵ��4+2$\sqrt{5}$��4-2$\sqrt{5}$��4��-1��
��ͼ����ֱ֪��y=-$\frac{3}{4}$x+3�ֱ�x�ᡢy���ڵ�A��B��P��������y=-$\frac{1}{2}$x2+2x+5�ϵ�һ�����㣬�������Ϊa������P��ƽ����y���ֱ�߽�ֱ��y=-$\frac{3}{4}$x+3�ڵ�Q����PQ=BQʱ��a��ֵ��4+2$\sqrt{5}$��4-2$\sqrt{5}$��4��-1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com