
����Ŀ�����ж���ʵ����ѧ����չ�������������������������������ƹ������ë�������������Ϊ���˽�ѧ������������ϲ����������������![]() ��ѧ����ÿ��ѧ����ѡ��ֻ��ѡ���������е�һ�֣���
��ѧ����ÿ��ѧ����ѡ��ֻ��ѡ���������е�һ�֣���
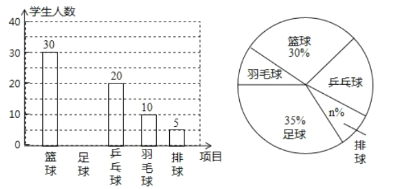
��������ͳ��ͼ�ṩ����Ϣ�������������⣺
��1��![]() ��
��![]() ��
��
��2����ȫ��ͼ�е�����ͳ��ͼ��
��3����ȫУ����![]() ��ѧ�����������УԼ�ж�����ѧ��ϲ����ƹ����
��ѧ�����������УԼ�ж�����ѧ��ϲ����ƹ����
��4���ڳ���![]() ��ѧ���У���Сޱ��С�ࡢС�졢С÷��
��ѧ���У���Сޱ��С�ࡢС�졢С÷��![]() ��ѧ��ϲ����ë����ѧУ�����Сޱ��С�ࡢС�졢С÷��
��ѧ��ϲ����ë����ѧУ�����Сޱ��С�ࡢС�졢С÷��![]() ��Ů���У�ѡȡ
��Ů���У�ѡȡ![]() ���μ�ȫ����ѧ��Ů����ë������������б�������״ͼ������ͬʱѡ��С�졢С��ĸ��ʣ����������У��ɽ�Сޱ��С�ࡢС�졢С÷�ֱ�����ĸ
���μ�ȫ����ѧ��Ů����ë������������б�������״ͼ������ͬʱѡ��С�졢С��ĸ��ʣ����������У��ɽ�Сޱ��С�ࡢС�졢С÷�ֱ�����ĸ![]() ��
��![]() ��
��![]() ��
��![]() ������
������
���𰸡���1��100��5����2������35�ˣ�ͼ����������3��400�ˣ���4��![]() .
.
��������
��1������30��ռ30%���ɵ����������ɴ˿��Լ����n��
��2�������������=100-30-20-10-5=35�ˣ����ɽ�����⣻
��3�����������������˼�뼴�ɽ�����⣮
��4��������״ͼ���ɽ�����⣮
�⣺��1��������m=30��30%=100������ռ![]() =5%
=5%
��n=5��
�ʴ�Ϊ100��5��
��2������=100-30-20-10-5=35�ˣ�
����ͼ��ͼ��ʾ��
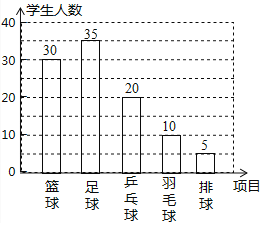
��3����ȫУ����2000��ѧ������УԼ��2000��![]() =400��ѧ��ϲ����ƹ����
=400��ѧ��ϲ����ƹ����
��4������״ͼ�ã�
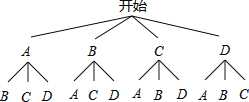
��һ����12�ֿ��ܳ��ֵĽ�������Ƕ��ǵȿ��ܵģ����������������֣�
��P��B��C���˽��б�����=![]() =
=![]() ��
��


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A������Ϊ��0��7������B������Ϊ��0��3������C������Ϊ��3��0����

��1����ͼ��������ABC�����Բ��������Ҫ����ͼ�ۼ�����д��������Բ������Ϊ ______��
��2������x�������������һ��D���ҡ�ADB=��ACB�����D������Ϊ ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y= ![]() +��1-2a��x��a��0��������˵��������ǣ�������
+��1-2a��x��a��0��������˵��������ǣ�������
A. ��![]() ʱ���ö��κ���ͼ��ĶԳ���Ϊy��
ʱ���ö��κ���ͼ��ĶԳ���Ϊy��
B. ��a��![]() ʱ���ö��κ���ͼ��ĶԳ�����y����Ҳ�
ʱ���ö��κ���ͼ��ĶԳ�����y����Ҳ�
C. �ö��κ�����ͼ��ĶԳ����Ϊx=1
D. ��x��2ʱ��y��ֵ��x��ֵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڵ����������ڳ��Ե��ӡ��ֻ���������Ϸ�ȣ������ս����ˣ�����Ϊ�˽�ѧ���������仯�������ȫ�а��꼶�����ȡ��1200��ѧ����ͳ����ÿ�������������������Ľ��������������4.9���µ������仯�Ƴ�����ͳ��ͼ�����������½�����Ҫ���ؽ��е��飬�Ƴ�����ͳ��ͼ.

����������⣺
��1��ͼ�С��������������ε�Բ�ĽǶ���Ϊ ��
��2����2016��ȫ�а��꼶ѧ������24000�����������������4.9���µ�ѧ��Լ�ж�������
��3����������ͳ��ͼ��Ϣ������Ϊ�����ѧ�������½�����Ҫ��������ʲô���������ѧ��Ӧ����α���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD������AD��AB�ij��ֱ�Ϊ3��8����B��C��x��ĸ������ϣ�E��DC���е㣬����������y��![]() ��x��0����ͼ����E����AB���ڵ�F��
��x��0����ͼ����E����AB���ڵ�F��
��1������B����Ϊ����6��0������m��ֵ��
��2����AF��AE��2���ҵ�E�ĺ�����Ϊa�����F�ĺ�����Ϊ�� �����ú�a�Ĵ���ʽ��ʾ������F��������Ϊ�� ���������������ı���ʽΪ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ�����
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
�����н��ۣ�
��ac��0��
�ڵ�x��1ʱ��y��ֵ��xֵ���������С��
��x��3�Ƿ���ax2+��b��1��x+c��0��һ������
�ܵ���1��x��3ʱ��ax2+��b��1��x+c��0��
С����������ѡȡһ�����ۣ���ѡ����ȷ���۵ĸ���Ϊ�� ��
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B�������120ǧ�ף��ס���������ͬһ����·��A�س�����B�أ��������г�������Ħ�г�,ͼ��DE��OC�ֱ��ʾ�ס����뿪A�ص�·��s����λ��ǧ�ף���ʱ��t����λ��Сʱ���ĺ�����ϵ��ͼ��������������У��ס����������y����λ��ǧ�ף�����y����t�ĺ���ͼ���ǣ� ��
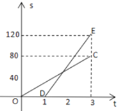
A. 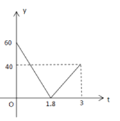 B.
B.  C.
C. 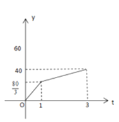 D.
D. 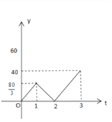
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C�ֱ���x�ᣬy����������ϣ���OA=4��OC=3���������߾���O��A���㣬�Ҷ�����BC���ϣ��Գ��ύBE�ڵ�F����D��E������ֱ�Ϊ��3��0������0��1����
��1���������ߵĽ���ʽ��
��2��������EDB����״������֤����
��3����M�ڶԳ����Ҳ���������ϣ���N��x���ϣ������Ƿ�����Ե�A��F��M��NΪ������ı�����ƽ���ı��Σ������ڣ���������з��������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD��AB��AC����E��F�ֱ���BC��AD���е㣬����AE��CF.
(1)��֤���ı���AECF�Ǿ��Σ�
(2)��AB��8������������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com