
如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.

(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若tan∠A=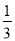 ,BC=8,求⊙O的半径.
,BC=8,求⊙O的半径.
(1)证明见解析;(2)⊙O的半径是6.
【解析】
试题分析:(1)根据等腰三角形的性质求得∠OBP+∠CBP=90°,则BC是⊙O的切线;
(2)根据锐角三角函数定义,可设OP=x,则OA=3x.在Rt△OBC中,由勾股定理列出关于x的方程(x+8)2=(3x)2+82,通过解该方程可以求得x=2,则OA=3x=6.
试题解析:(1)相切.理由如下:
∵OA=OB,
∴∠A=∠OBA.
∵CP=BP,
∴∠CBP=∠BPC.
∵∠OPA=∠BPC,∠A+∠OPA=90°,
∴∠OBP+∠CBP=90°,
∴BC是⊙O的切线;
(2)∵tanA=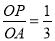 ,
,
∴设OP=x,则OA=3x.
在Rt△OBC中,(x+8)2=(3x)2+82,
解得 x=2,则OA=6,
∴⊙O的半径是6.
考点:1.切线的判定2.勾股定理.


科目:初中数学 来源:2013-2014学年江苏省南京市溧水区中考一模数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,已知点A(2,0),⊙A的半径是2,⊙P的半径是1,满足与⊙A及y轴都相切的⊙P有 个.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:解答题
如图,抛物线y=-x2+bx+c与x轴交于点A(1,0)、C,交y轴于点B,对称轴x=-1与x轴交于点D.
(1)求该抛物线的解析式和B、C点的坐标;
(2)设点P(x,y)是第二象限内该抛物线上的一个动点,△PBD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围;

(3)点G在x轴负半轴上,且∠GAB=∠GBA,求G的坐标;
(4)若此抛物线上有一点Q,满足∠QCA=∠ABO,若存在,求直线QC的解析式;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:选择题
下列各式计算正确的是( )
A.a3+2a2=3a6 B.3 +4
+4 =7
=7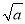 C.a4•a2=a8 D.(ab2)3=ab6
C.a4•a2=a8 D.(ab2)3=ab6
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(二模)数学试卷(解析版) 题型:填空题
如图,数轴上M、N两点表示的数分别为 和5.2,则M、N两点之间表示整数的点共有 个.
和5.2,则M、N两点之间表示整数的点共有 个.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏大丰刘庄第二初中九年级下学期第一次月考数学试卷(解析版) 题型:解答题
在一个不透明的袋子中装有3个除颜色外完全相同的小球,其中白球1个、黄球1个、红球1个,摸出一个球记下颜色后放回,再摸出一个球,记下相应颜色.
(1)请用列表法或画树状图法表示出两次所得颜色的所有可能情形;
(2)求两次摸到的球同色的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏仪征大仪中学九年级3月月考数学试卷(解析版) 题型:选择题
如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,它的方向是( )


A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com