
如图,抛物线y=-x2+bx+c与x轴交于点A(1,0)、C,交y轴于点B,对称轴x=-1与x轴交于点D.
(1)求该抛物线的解析式和B、C点的坐标;
(2)设点P(x,y)是第二象限内该抛物线上的一个动点,△PBD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围;

(3)点G在x轴负半轴上,且∠GAB=∠GBA,求G的坐标;
(4)若此抛物线上有一点Q,满足∠QCA=∠ABO,若存在,求直线QC的解析式;若不存在,试说明理由.
(1)y=-x2-2x+3,C(-3,0)、B(0,3);(2)S=- x2-
x2- (-3<x<0);(3)G(-4,0);(4)存在,
(-3<x<0);(3)G(-4,0);(4)存在, ,或
,或 .
.
【解析】
试题分析:(1)先根据抛物线y=-x2+bx+c与x轴交于点A(1,0),对称轴为x=-1,列出关于b、c的方程组,解方程组求出b、c的值,得到抛物线的解析式为y=-x2-2x+3;再解方程-x2-2x+3=0,求出x的值,得到C点的坐标;将x=0代入y=-x2-2x+3,求出y的值,得到B点的坐标;
(2)过点P作PE⊥x轴于点E,根据S=S梯形PEOB-S△BOD-S△PDE求出S关于x的函数关系式,再根据点P(x,y)是第二象限内该抛物线上的一个动点,得出自变量x的取值范围;
(3)设G点坐标为(a,0),则a<0.根据等角对等边得出GB=GA,由此列出方程a2+32=(1-a)2,解方程求出a的值,即可得到G点坐标;
(4)先根据正切函数的定义得出tan∠ABO= ,由于∠QCA=∠ABO,得到tan∠QCA=
,由于∠QCA=∠ABO,得到tan∠QCA= ,再由直线斜率的意义可知直线QC的斜率|k|=
,再由直线斜率的意义可知直线QC的斜率|k|= ,则k=±
,则k=± .由此可设直线QC的解析式为y=
.由此可设直线QC的解析式为y= x+n,或y=-
x+n,或y=- x+n,然后将C点坐标(-3,0)代入,求出n的值,即可得到直线QC的解析式.
x+n,然后将C点坐标(-3,0)代入,求出n的值,即可得到直线QC的解析式.
试题解析:(1) b=-2,c=3 ,C(-3,0)、B(0,3)
(2)过点P作PE⊥x轴于点E.
S=S梯形PEOB﹣S△BOD﹣S△PDE= .
.
将y=-x2-2x+3代入得S=- x2-x+
x2-x+ -
- ﹣
﹣ =-
=- x2-
x2- x.
x.
∴-3<x<0.
∴S关于x的函数关系式为:S=- x2-
x2- (-3<x<0).
(-3<x<0).
(3)G(-4,0)
(4)存在
直线QC解析式为 ,或
,或 .
.
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年江苏省句容市九年级下学期期中考试(即一模)数学试卷(解析版) 题型:选择题
如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为
A. B.
B. C.
C. D.
D.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:选择题
点O1、O2在直线l上,⊙O1的半径为2 cm,⊙O2的半径为3 cm,4 cm<O1O2<8 cm.⊙O1与⊙O2
不可能出现的位置关系是( )
A.外离 B.外切 C.相交 D.内切
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:解答题
果农李明种植的草莓计划以每千克15元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,对价格经过两次下调后,以每千克9.6元的单价对外批发销售.
(1)求李明平均每次下调的百分率;
(2)小刘准备到李明处购买3吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金400元.
试问小刘选择哪种方案更优惠,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:填空题
小明从点O出发,沿直线前进10米,向左转n°(0<n<180),再沿直线前进10米,又向左转n°……照这样走下去,小明恰能回到O点,且所走过的路程最短,则n的值等于 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(二模)数学试卷(解析版) 题型:解答题
如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.

(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若tan∠A=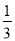 ,BC=8,求⊙O的半径.
,BC=8,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com