
【题目】如图,在⊙O中,弦AB、CD相交于点E,且AB=CD,∠BED=α(0°<α<180°).有下列结论:①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=![]() .其中一定成立的个数为( )
.其中一定成立的个数为( )

A.3个B.2个C.1个D.0个
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
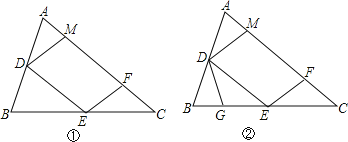
【题目】在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.

(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC.
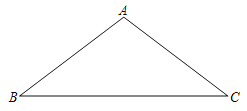
(1)用无刻度的直尺和圆规作△ABC的外接圆;(保留画图痕迹)
(2)若AB=10,BC=16,求△ABC的外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)B点的对应点B′的坐标是 ;C点的对应点C′的坐标是 ;
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现将标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上,所有卡片的形状、大小都完全相同.现随机从中抽取一张卡片将其上面的数字作为十位上的数,然后放回洗匀,再随机抽取一张卡片,将其上面的数字作为个位上的数,组成两位数.
(1)请用列表或画树状图的方法表示出所有可能出现的结果:
(2)求这个两位数恰好能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com