
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
【答案】(1)y1=2x+6;(2)y2=![]() x2﹣
x2﹣![]() x+
x+![]() ;(3)w=﹣
;(3)w=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ,7月份销售每千克猪肉所第获得的利润最大,最大利润是77元7.
,7月份销售每千克猪肉所第获得的利润最大,最大利润是77元7.
【解析】
(1)设![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,将(3,12)(4,14)代入
,将(3,12)(4,14)代入![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)由题意得到抛物线的顶点坐标为(3,9),设![]() 与x之间的函数关系式为:
与x之间的函数关系式为:![]() =
=![]() ,将(5,10)代入
,将(5,10)代入![]() =
=![]() 得
得![]() =10,解方程即可得到结论;
=10,解方程即可得到结论;
(3)由题意得到w=![]()
![]() =2x+6
=2x+6![]()
![]() +
+![]() x
x![]() =
=![]()
![]() +
+![]() x
x![]() ,根据二次函数的性质即可得到结论.
,根据二次函数的性质即可得到结论.
(1)设y1与x之间的函数关系式为y1=kx+b,
将(3,12)(4,14)代入y1得,![]() ,
,
解得:![]() ,
,
∴y1与x之间的函数关系式为:y1=2x+6;
(2)由题意得,抛物线的顶点坐标为(3,9),
∴设y2与x之间的函数关系式为:y2=a(x﹣3)2+9,
将(5,10)代入y2=a(x﹣3)2+9得a(5﹣3)2+9=10,
解得:a=![]() ,
,
∴y2=![]() (x﹣3)2+9=
(x﹣3)2+9=![]() x2﹣
x2﹣![]() x+
x+![]() ;
;
(3)由题意得,w=y1﹣y2=2x+6﹣![]() x2+
x2+![]() x﹣
x﹣![]() =﹣
=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ,
,
∵﹣![]() <0,
<0,
∴w由最大值,
∴当x=﹣![]() =﹣
=﹣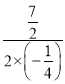 =7时,w最大=﹣
=7时,w最大=﹣![]() ×72+
×72+![]() ×7﹣
×7﹣![]() =7.
=7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于点A(﹣2,0)与点C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
的图象与x轴交于点A(﹣2,0)与点C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
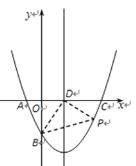
(1)求该二次函数的解析式;
(2)若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB, PD,BD,AB.请问是否存在点P,使得△BDP的面积恰好等于△ADB的面积?若存在请求出此时点P的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象经过点C(0,-2),顶点D的坐标为(1,
的图象经过点C(0,-2),顶点D的坐标为(1,![]() ),与
),与![]() 轴交于A、B两点.
轴交于A、B两点.
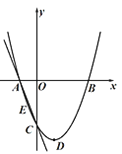
(1)求抛物线的解析式.
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和![]() 的值.
的值.
(3)点F(0,![]() )是
)是![]() 轴上一动点,当
轴上一动点,当![]() 为何值时,
为何值时,![]() 的值最小.并求出这个最小值.
的值最小.并求出这个最小值.
(4)点C关于![]() 轴的对称点为H,当
轴的对称点为H,当![]() 取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)(2015黄石)如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.

(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
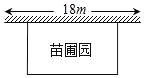
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为 30 米的篱笆 围成.已知墙长为 18 米(如图所示),设这个苗圃园垂直于墙的一边的长为 x 米,若平行于墙的一边长不小 于 8 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣1)2+4的图象经过点(﹣1,0).
(1)求这个二次函数的解析式;
(2)判断这个二次函数的开口方向,对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣4ax+3a.
(1)若a=1,则函数y的最小值为_______.
(2)当1≤x≤4时,y的最大值是4,则a的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com