
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于点A(﹣2,0)与点C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
的图象与x轴交于点A(﹣2,0)与点C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
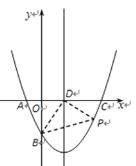
(1)求该二次函数的解析式;
(2)若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB, PD,BD,AB.请问是否存在点P,使得△BDP的面积恰好等于△ADB的面积?若存在请求出此时点P的坐标,若不存在说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)存在,P点坐标为(
x﹣4;(2)存在,P点坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)利用待定系数法求抛物线的解析式;
(2)先确定抛物线的对称轴得到D(3,0),再确定B(0,-4),连接OP,如图,设P(m,![]() m2-
m2-![]() m-4)(0<m<8),利用S△PBD=S△POD+S△POB-S△BOD=
m-4)(0<m<8),利用S△PBD=S△POD+S△POB-S△BOD=![]() ×3×(-
×3×(-![]() m2+
m2+![]() m+4)+
m+4)+![]() ×4×m-
×4×m-![]() ×3×4=
×3×4=![]() ×5×4得到关于m的方程,然后解方程求出m即可得到P点坐标.
×5×4得到关于m的方程,然后解方程求出m即可得到P点坐标.
解:(1)把A(﹣2,0)和C(8,0)代入y=ax2+bx﹣4得![]() ,解得
,解得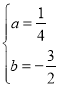 ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)存在.
∵y=![]() x2﹣
x2﹣![]() x﹣4=
x﹣4=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ,
,
∴抛物线的对称轴为直线x=3,
∴D(3,0),
当x=0时,y=![]() x2﹣
x2﹣![]() x﹣4=﹣4,则B(0,﹣4),
x﹣4=﹣4,则B(0,﹣4),
连接OP,如图,设P(m,![]() m2﹣
m2﹣![]() m﹣4)(0<m<8),
m﹣4)(0<m<8),
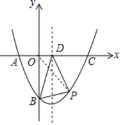
∵S△PBD=S△POD+S△POB﹣S△BOD,S△ABD=![]() ×5×4=10,
×5×4=10,
而△BDP的面积恰好等于△ADB的面积,
∴![]() ×3×(﹣
×3×(﹣![]() m2+
m2+![]() m+4)+
m+4)+![]() ×4×m﹣
×4×m﹣![]() ×3×4=10,
×3×4=10,
整理得3m2﹣34m+80=0,解得m1=![]() ,m2=8(舍去),
,m2=8(舍去),
∴P点坐标为(![]() ,﹣
,﹣![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
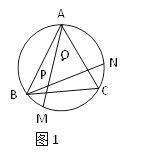
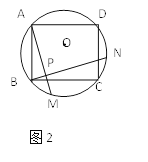
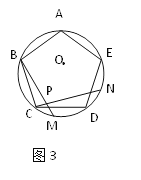

(1)求图1中∠APN的度数;
(2)图2中,∠APN的度数是_______,图3中∠APN的度数是________。
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
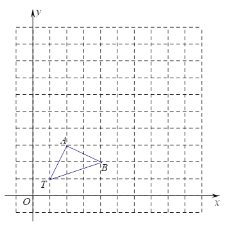
【题目】如图,在11×11的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1,在位似中心的同侧将△TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;点A′的坐标为 ,点B′的坐标为
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学毕业生响应国家“自主创业”的号召,投资开办了一个装怖品商店,该店采购了一种今年新上市的装饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件),销售价格Q(元/件)与销售时间x(天) (1≤x≤30,且x为正整数)都满足一次函数关系,其函数图象如图所示:
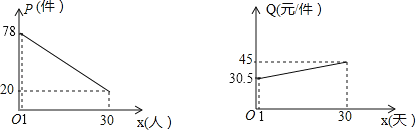
(1)请直接写出:销售量(P件)与销售时间x(天)之间的函数关系式,销售价格Q(元/件)与销售时间x(天)之间的函数关系式;
(2)请问在30天的试销售中,哪﹣天的日销售利润最大?求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,《九章算术》是我国古代数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过点A(1,0)和点C(0,3),对称轴为直线x=1.
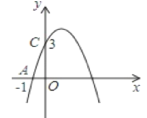
(1)求该二次函数的关系式和顶点坐标;
(2)结合图象,解答下列问题:
①当1<x<2时,求函数y的取值范围。
②当y<3时,求x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
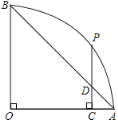
【题目】如图,扇形OAB中,∠AOB=90°.P为弧AB上的一点,过点P作PC⊥OA,垂足为C,PC与AB交于点D.若PD=2,CD=1,则该扇形的半径长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com