
����Ŀ����ͼ����11��11�������������У���TAB�Ķ���ֱ�ΪT��1��1����A��2��3����B��4��2����
��1���Ե�T��1��1��Ϊλ�����ģ��������ߣ�TA����TA��3��1����λ�����ĵ�ͬ�ཫ��TAB�Ŵ�Ϊ��TA��B�����Ŵ���A��B�Ķ�Ӧ��ֱ�ΪA����B����������TA��B������д����A����B�������ꣻ��A��������Ϊ ����B��������Ϊ
��2���ڣ�1���У���C��a��b��Ϊ�߶�AB����һ�㣬д���仯���C�Ķ�Ӧ��C��������Ϊ ��
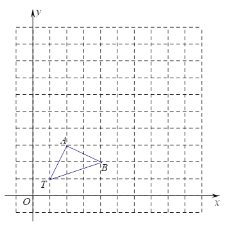
���𰸡���1��������;��2��C��(3a-2,3b-2).
��������
��1��������Ŀ����������λ�����ĵ�ͬ�ཫ��TAB�Ŵ�Ϊԭ����3�����õ���Ӧ�����꣬��ȷ������ͼ�μ��ɣ�����ͼ��ȷ����������꼴�ɣ�
��2�����ݣ�1���б任�Ĺ��ɣ�����д���仯���C�Ķ�Ӧ��C�������꣮
�⣺��1����ͼ��ʾ��
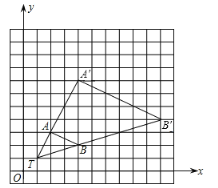
��A����B��������ֱ�Ϊ��A����4��7����B����10��4����
�ʴ�Ϊ��4��7��10��4��
��2���仯���C�Ķ�Ӧ��C��������Ϊ��C����3a-2��3b-2��
�ʴ�Ϊ��3a-2��3b-2��


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�ABC��ֱ���AB��ACΪ������AEB���AFC��
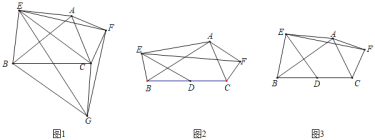
��1����ͼ1����AEB���AFC�ֱ�����AB��ACΪб�ߵĵ���ֱ�������Σ�����EF����EFΪֱ�DZ߹���Rt��EFG����EF��FG������BG��CG��EC��
��֤���١�AEF�ա�CGF�����ı���BGCE��ƽ���ı��Σ�
��2��С���ܵ�ͼ1���������˽�һ��̽����
��ͼ2���ڡ�ABC��ֱ���AB��ACΪб����Rt��AEB��Rt��AFC����ʹ��FAC����EAB��30�㣬ȡBC���е�D������DE��EF���֣��������һ����������ϵ�ҼнǶ���һ�����������С�����![]() ��ֵ����DEF�Ķ�����
��ֵ����DEF�Ķ�����
��3��Сӱ�ܵ�����Ҳ����̽����
��ͼ3���ڡ�ABC��ֱ���AB��ACΪ�ױ�������������AEB�͵���������AFC����ʹ��CAF+��EAB��90�㣬ȡBC���е�D������DE��EF���֣���������EAB����ʱ������Ҳ����һ����������ϵ�ҼнǶ���һ������AE��m��AB��n���������Сӱ�ú�m��n�Ĵ���ʽֱ��д��![]() ��ֵ�����ú����Ĵ���ʽֱ�ӱ�ʾ��DEF�Ķ�����
��ֵ�����ú����Ĵ���ʽֱ�ӱ�ʾ��DEF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��ʼ�ر�
��ʼ�ر�![]() ���
���![]() ��
��![]() ���ٶ��ƶ������ͬʱ����
���ٶ��ƶ������ͬʱ����![]() �ӵ�
�ӵ�![]() ��ʼ�ر�
��ʼ�ر�![]() ���
���![]() ��
��![]() ���ٶ��ƶ�����
���ٶ��ƶ�����![]() ��
��![]() �ֱ��
�ֱ��![]() ��
��![]() ͬʱ�������˶�ʱ��Ϊ
ͬʱ�������˶�ʱ��Ϊ![]() ��������һ���ȵ����յ�ʱ����һ��Ҳֹͣ�˶�������������⣺
��������һ���ȵ����յ�ʱ����һ��Ҳֹͣ�˶�������������⣺
��1���������룬![]() ���������
���������![]() ��
��
��2���Ƿ����������ʱ��![]() ��ʹ�߶�
��ʹ�߶�![]() ǡ��ƽ��
ǡ��ƽ��![]() ������������ڣ�����˶�ʱ��
������������ڣ�����˶�ʱ��![]() ���������ڣ���˵�����ɣ�
���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
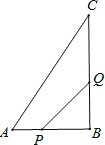
����Ŀ����ͼ��ֱ��y����x+4��x�ύ�ڵ�B����y�ύ�ڵ�C��������y����x2+bx+c����B��C���㣬��x����һ����ΪA����P��ÿ��![]() ����λ���ȵ��ٶ����߶�BC���ɵ�B���C�˶�����P�����B�͵�C�غϣ������˶�ʱ��Ϊt�룬����P��x�ᴹ�߽�x���ڵ�E�����������ڵ�M��
����λ���ȵ��ٶ����߶�BC���ɵ�B���C�˶�����P�����B�͵�C�غϣ������˶�ʱ��Ϊt�룬����P��x�ᴹ�߽�x���ڵ�E�����������ڵ�M��
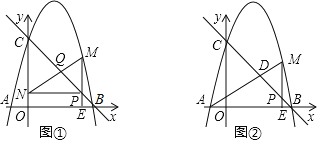
��1���������ߵĽ���ʽ��
��2����ͼ��������P��y�ᴹ�߽�y���ڵ�N������MN��BC�ڵ�Q����![]() ʱ����t��ֵ��
ʱ����t��ֵ��
��3����ͼ��������AM��BC�ڵ�D������PDM�ǵ���������ʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ͷ��1��ԪΧһ�����β�(��ͼ)������һ�߿�ǽ����������ѡ�ò�ͬ���Ͻ���.ǽ��24 m��ƽ����ǽ�ıߵķ���Ϊ200Ԫ/m����ֱ��ǽ�ıߵķ���Ϊ150Ԫ/m����ƽ����ǽ�ı߳�Ϊx m.
(1)�费ֱ��ǽ��һ�߳�Ϊy m��ֱ��д��y��x֮��ĺ�����ϵʽ��
(2)�������Ϊ384 m2����x��ֵ��
(3)�����������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���ACB=90����AC=6cm��BC=8cm����P��A������AC��C����1����/����ٶ������ƶ�����Q��C������CB��B����2����/��� �ٶ������ƶ�����P��Q�ֱ�����ͬʱ�������ƶ���ijһλ��ʱ����ʱ��Ϊt�룮
��1����t= ʱ��PQ��AB
��2����tΪ��ֵʱ����PCQ���������5cm2��
��3����P��Q�˶������У���ijһʱ�̣�������PQC���ۣ��õ���EPQ����ͼ2��PE��AB�ܷ�ֱ�����ܣ������Ӧ��tֵ�������ܣ���˵�����ɣ�
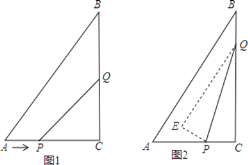
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x��1����x���һ����������Ϊ����1��0������y�ύ��Ϊ��0��3�����䲿��ͼ����ͼ��ʾ�������н��۴�����ǣ�������
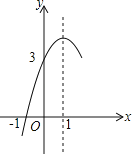
A. b![]() ��4ac��0
��4ac��0
B. ����x�ķ���ax![]() +bx+c��3��0����������ȵ�ʵ����
+bx+c��3��0����������ȵ�ʵ����
C. a��b+c��0
D. ��y��0ʱ����1��x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ�ڵ�A����2��0�����C��8��0�����㣬��y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
��ͼ����x�ύ�ڵ�A����2��0�����C��8��0�����㣬��y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
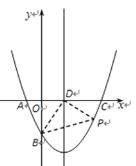
��1����ö��κ����Ľ���ʽ��
��2������P��m��n���Ǹö��κ���ͼ���ϵ�һ�����㣨����m��0��n��0��������PB�� PD��BD��AB�������Ƿ���ڵ�P��ʹ����BDP�����ǡ�õ�����ADB��������������������ʱ��P�����꣬��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ͼ����C(0��-2)������D������Ϊ��1��
��ͼ����C(0��-2)������D������Ϊ��1��![]() ������
������![]() �ύ��A��B����.
�ύ��A��B����.
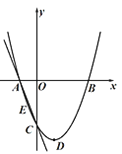
��1���������ߵĽ���ʽ.
��2������AC��EΪֱ��AC��һ�㣬����AOC�ס�AEBʱ�����E�������![]() ��ֵ.
��ֵ.
��3����F��0��![]() ����
����![]() ����һ���㣬��
����һ���㣬��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��ֵ��С.����������Сֵ.
��ֵ��С.����������Сֵ.
��4����C����![]() ��ĶԳƵ�ΪH����
��ĶԳƵ�ΪH����![]() ȡ��Сֵʱ���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��QHF��ֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵������.
ȡ��Сֵʱ���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��QHF��ֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com