
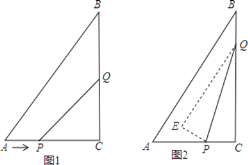
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的 速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
(1)当t= 时,PQ∥AB
(2)当t为何值时,△PCQ的面积等于5cm2?
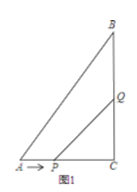
(3)在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
【答案】(1)2.4;(2)1;(3)见解析.
【解析】
(1)由PQ∥AB得出△PQC∽△ABC,从而得到比例式PC:AC=CQ:BC,建立关于t的方程,解方程求出t的值即可;
(2)由三角形面积公式可建立关于t的方程,解方程求出t的值即可;
(3)延长QE交AC于点D,若PE⊥AB,则QD∥AB,所以可得△CQD∽△CBA,由相似三角形的性质:对应边的比值相等可求出DE=0.5t,易证△ABC∽△DPE,再由相似三角形的性质可得![]() ,把已知数据代入即可求出t的值.
,把已知数据代入即可求出t的值.
解:(1) ∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴PC=AC-AP=6-t,CQ=2t,
当PQ∥AB时,∴△PQC∽△ABC,
∴PC:AC=CQ:BC,
∴(6-t):6=2t:8
∴t=2.4
∴当t=2.4时,PQ∥AB
(2)∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴PC=AC-AP=6-t,CQ=2t,
∴S△CPQ=![]() CPCQ=
CPCQ=![]() =5,
=5,
∴t2-6t+5=0
解得t1=1,t2=5(不合题意,舍去)
∴当t=1秒时,△PCQ的面积等于5cm2;
(3)能垂直,理由如下:
延长QE交AC于点D,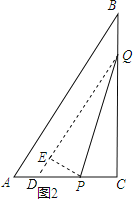
∵将△PQC翻折,得到△EPQ,
∴△QCP≌△QEP,
∴∠C=∠QEP=90°,
若PE⊥AB,则QD∥AB,
∴△CQD∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴QD=2.5t,
∵QC=QE=2t
∴DE=0.5t
∵∠A=∠EDP,∠C=∠DEP=90°,
∴△ABC∽△DPE,
∴![]()
∴![]() ,
,
解得:![]() ,
,
综上可知:当t=![]() 时,PE⊥AB.
时,PE⊥AB.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】下列给定的三点能确定一个圆的是( )
A. 线段![]() 的中点
的中点![]() 及两个端点
及两个端点
B. 角的顶点及角的边上的两点
C. 三角形的三个顶点
D. 矩形的对角线交点及两个顶点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知二次函数![]() .以下四个结论:
.以下四个结论:
①不论![]() 取何值,图象始终过点(
取何值,图象始终过点(![]() ,
,![]() );
);
②当![]() 时,抛物线与
时,抛物线与![]() 轴没有交点:
轴没有交点:
③当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
④当![]() 时,抛物线的顶点达到最高位置.
时,抛物线的顶点达到最高位置.
请你分别判断四个结论的真假,并给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有点A(-4,0)、B(0,3)、P(a,-a)三点,线段CD与AB关于点P中心对称,其中A、B的对应点分别为C、D
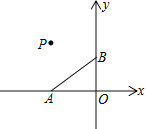
(1) 当a=-4时
① 在图中画出线段CD,保留作图痕迹
② 线段CD向下平移 个单位时,四边形ABCD为菱形
(2) 当a=___________时,四边形ABCD为正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
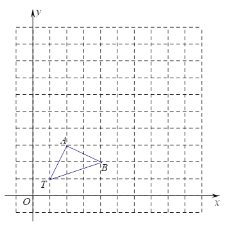
【题目】如图,在11×11的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1,在位似中心的同侧将△TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;点A′的坐标为 ,点B′的坐标为
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O是△ABC的外接圆,AB是直径,D是⊙O外一点且满足∠DCA=∠B,连接AD.
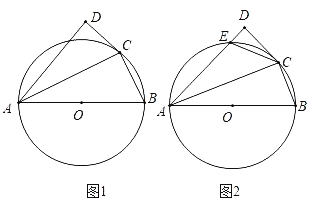
(1)求证:CD是⊙O的切线;
(2)若AD⊥CD,CD=2,AD=4,求直径AB的长;
(3)如图2,当∠DAB=45°时,AD与⊙O交于E点,试写出AC、EC、BC之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学毕业生响应国家“自主创业”的号召,投资开办了一个装怖品商店,该店采购了一种今年新上市的装饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件),销售价格Q(元/件)与销售时间x(天) (1≤x≤30,且x为正整数)都满足一次函数关系,其函数图象如图所示:
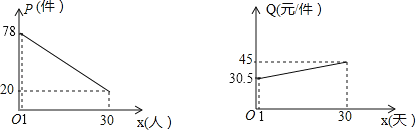
(1)请直接写出:销售量(P件)与销售时间x(天)之间的函数关系式,销售价格Q(元/件)与销售时间x(天)之间的函数关系式;
(2)请问在30天的试销售中,哪﹣天的日销售利润最大?求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过点A(1,0)和点C(0,3),对称轴为直线x=1.
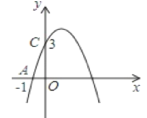
(1)求该二次函数的关系式和顶点坐标;
(2)结合图象,解答下列问题:
①当1<x<2时,求函数y的取值范围。
②当y<3时,求x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
七年级: 76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
八年级: 74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整,整理、描述数据:
|
|
|
|
| |
七年级 | 1 | 2 | 6 | ||
八年级 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 84 | 88.5 | |
八年级 | 84.2 | 74 |
(2)为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据______来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);
(3)若八年级有800名学生,试估计八年级学生成绩优秀的人数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com