
【题目】已知:在△ABC外分别以AB,AC为边作△AEB与△AFC.
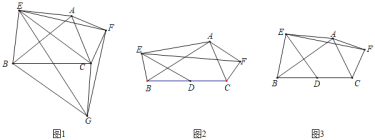
(1)如图1,△AEB与△AFC分别是以AB,AC为斜边的等腰直角三角形,连接EF.以EF为直角边构造Rt△EFG,且EF=FG,连接BG,CG,EC.
求证:①△AEF≌△CGF;②四边形BGCE是平行四边形.
(2)小明受到图1的启发做了进一步探究:
如图2,在△ABC外分别以AB,AC为斜边作Rt△AEB与Rt△AFC,并使∠FAC=∠EAB=30°,取BC的中点D,连接DE,EF后发现,两者间存在一定的数量关系且夹角度数一定,请你帮助小明求出![]() 的值及∠DEF的度数.
的值及∠DEF的度数.
(3)小颖受到启发也做了探究:
如图3,在△ABC外分别以AB,AC为底边作等腰三角形AEB和等腰三角形AFC,并使∠CAF+∠EAB=90°,取BC的中点D,连接DE,EF后发现,当给定∠EAB=α时,两者间也存在一定的数量关系且夹角度数一定,若AE=m,AB=n,请你帮助小颖用含m,n的代数式直接写出![]() 的值,并用含α的代数式直接表示∠DEF的度数.
的值,并用含α的代数式直接表示∠DEF的度数.
【答案】(1)①见解析;②见解析;(2)![]() =
=![]() ;(3)cos∠DEF=
;(3)cos∠DEF=![]() .
.
【解析】
(1)①根据SAS即可证明三角形全等.
②想办法证明BE=CG,BE∥CG即可.
(2)如图2中,延长ED到G,使得DG=ED,连接CG,FG.证明△CGF∽△AEF,推出![]() ,∠CFG=∠AFE,推出∠EFG=∠CFG+∠EFC=∠AFE+∠EFC=90°,推出tan∠DEF=
,∠CFG=∠AFE,推出∠EFG=∠CFG+∠EFC=∠AFE+∠EFC=90°,推出tan∠DEF=![]() ,可得∠DEF=30°即可解决问题.
,可得∠DEF=30°即可解决问题.
(3)如图3中,延长ED到G,使得DG=ED,连接CG,FG.作EH⊥AB于H,连接FD.想办法证明∠AEH=∠DEF,利用勾股定理求出EH,即可解决问题.
(1)证明:①如图1中,
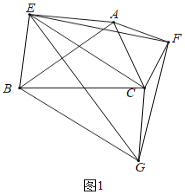
∵△EFC与△AFC都是等腰直角三角形,
∴FA=FC,FE=FG,∠AFC=∠EFG=90°,
∴∠AFE=∠CFG,
∴△AFE≌△CFG(SAS).
②∵△AFE≌△CFG,
∴AE=CG,∠AEF=∠CGF,
∵△AEB是等腰直角三角形,
∴AE=BE,∠BEA=90°,
∴CG=BE,
∵△EFG是等腰直角三角形,
∴∠FEG=∠FGE=45°,
∴∠AEF+∠BEG=45°,
∵∠CGE+∠CGF=45°,
∴∠BEG=∠CGE,
∴BE∥CG,
∴四边形BECG是平行四边形.
(2)解:如图2中,延长ED到G,使得DG=ED,连接CG,FG.
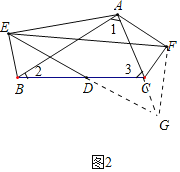
∵点D是BC的中点,
∴BD=CD,
∵∠EDB=∠GDC,
∴EB=GC,∠EBD=∠GCD,
在Rt△AEB与Rt△AFC中,
∵∠EAB=∠FAC=30°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠EBD=∠2+60°,
∴∠DCG=∠2+60°,
∴∠GCF=360°﹣60°﹣(∠2+60°)﹣∠3
=360°﹣120°﹣(∠2+∠3)
=360°﹣120°﹣(180°﹣∠1)
=60°+∠1,
∵∠EAF=30°+∠1+30°=60°+∠1,
∴∠GCF=∠EAF,
∴△CGF∽△AEF,
∴![]() ,∠CFG=∠AFE,
,∠CFG=∠AFE,
∴∠EFG=∠CFG+∠EFC=∠AFE+∠EFC=90°,
∴tan∠DEF=![]() ,
,
∴∠DEF=30°,
∴FG=![]() EG,
EG,
∵ED=![]() EG,
EG,
∴ED=FG,
∴![]() .
.
(3)如图3中,延长ED到G,使得DG=ED,连接CG,FG.作EH⊥AB于H,连接FD.
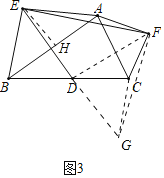
∵BD=DC,∠BDE=∠CDG,DE=DG,
∴△CDG≌△BDE(SAS),
∴CG=BE=AE,∠DCG=∠DBE=α+∠ABC,
∵∠GCF=360°﹣∠DCG﹣∠ACB﹣∠ACF=360°﹣(α+∠ABC)﹣∠ACB﹣(90°﹣α)=270°﹣(∠ABC+∠ACB)=270°﹣(180°﹣∠BAC)=90°+∠BAC=∠EAF,
∴△EAF≌△GCF(SAS),
∴EF=GF,∠AFE=∠CFG,
∴∠AFC=∠EFC,
∴∠DEF=∠CAF=90°﹣α,
∵∠AEH=90°﹣α,
∴∠AEH=∠DEF,
∵AE=m,AH=![]() AB=
AB=![]() n,
n,
∴EH=![]() ,
,
∵DE=DG,EF=GF,
∴DF⊥EG,
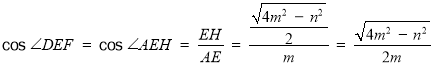 .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-(2k-1)x+k2,其中k是常数.
(1)若该抛物线与x轴有交点,求k的取值范围;
(2)若此抛物线与x轴其中一个交点的坐标为(-1,0),试确定k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
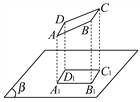
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
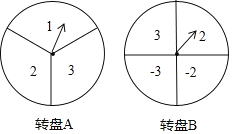
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列给定的三点能确定一个圆的是( )
A. 线段![]() 的中点
的中点![]() 及两个端点
及两个端点
B. 角的顶点及角的边上的两点
C. 三角形的三个顶点
D. 矩形的对角线交点及两个顶点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
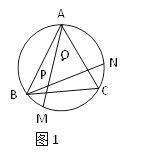
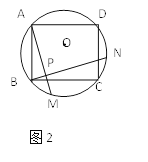
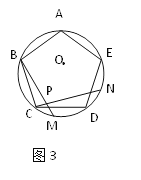

(1)求图1中∠APN的度数;
(2)图2中,∠APN的度数是_______,图3中∠APN的度数是________。
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
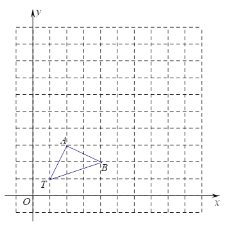
【题目】如图,在11×11的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1,在位似中心的同侧将△TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;点A′的坐标为 ,点B′的坐标为
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com