
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),与y轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( )
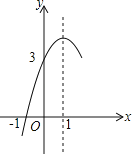
A. b![]() ﹣4ac≥0
﹣4ac≥0
B. 关于x的方程ax![]() +bx+c﹣3=0有两个不相等的实数根
+bx+c﹣3=0有两个不相等的实数根
C. a﹣b+c=0
D. 当y>0时,﹣1<x<3
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别是A(﹣1,1),B(﹣4,1),C(﹣3,3).
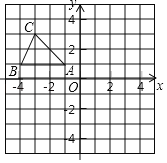
(1)将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;并判断以O,A1,B为顶点的三角形的形状(直接写出结果);
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2,并求出点C旋转到C2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
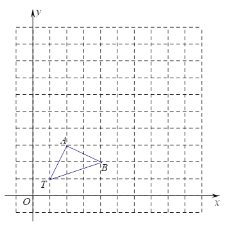
【题目】如图,在11×11的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1,在位似中心的同侧将△TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;点A′的坐标为 ,点B′的坐标为
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学毕业生响应国家“自主创业”的号召,投资开办了一个装怖品商店,该店采购了一种今年新上市的装饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件),销售价格Q(元/件)与销售时间x(天) (1≤x≤30,且x为正整数)都满足一次函数关系,其函数图象如图所示:
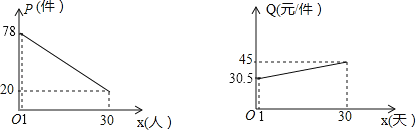
(1)请直接写出:销售量(P件)与销售时间x(天)之间的函数关系式,销售价格Q(元/件)与销售时间x(天)之间的函数关系式;
(2)请问在30天的试销售中,哪﹣天的日销售利润最大?求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,《九章算术》是我国古代数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
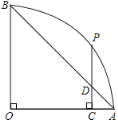
【题目】如图,扇形OAB中,∠AOB=90°.P为弧AB上的一点,过点P作PC⊥OA,垂足为C,PC与AB交于点D.若PD=2,CD=1,则该扇形的半径长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲![]() 如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元
如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元![]() 为整数
为整数![]() .
.
![]() 直接写出每天游客居住的房间数量y与x的函数关系式.
直接写出每天游客居住的房间数量y与x的函数关系式.
![]() 设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
![]() 某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人
某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人![]() 问:这天宾馆入住的游客人数最少有多少人?
问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com