
����Ŀ��ij������50�����乩�ο;�ס,��ÿ�����䶨��120Ԫʱ,�����ȫ��ס��,��ÿ������ÿ��Ķ���ÿ����10Ԫʱ,�ͻ���һ���������![]() ����ο;�ס����,�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ���,��ÿ�����䶨������10xԪ
����ο;�ס����,�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ���,��ÿ�����䶨������10xԪ![]() Ϊ����
����![]() ��
��
![]() ֱ��д��ÿ���ο;�ס�ķ�������y��x�ĺ�����ϵʽ��
ֱ��д��ÿ���ο;�ס�ķ�������y��x�ĺ�����ϵʽ��
![]() �����ÿ�������ΪWԪ,��ÿ�䷿�۶���Ϊ����Ԫʱ,����ÿ�������������,��������Ƕ��٣�
�����ÿ�������ΪWԪ,��ÿ�䷿�۶���Ϊ����Ԫʱ,����ÿ�������������,��������Ƕ��٣�
![]() ij��,�����˽���ס�����,�õ�������Ϣ���ٵ�������������5000Ԫ,�ڱ���Ϊ�ο;�ס�ķ��乲֧������û�г���600Ԫ,��ÿ������պ�ס��2��
ij��,�����˽���ס�����,�õ�������Ϣ���ٵ�������������5000Ԫ,�ڱ���Ϊ�ο;�ס�ķ��乲֧������û�г���600Ԫ,��ÿ������պ�ס��2��![]() �ʣ����������ס���ο����������ж����ˣ�
�ʣ����������ס���ο����������ж����ˣ�
���𰸡�(1)![]() ,
,![]() ,��x����
,��xΪ����![]() ��(2)��ÿ�䷿�۶���Ϊ320Ԫʱ,����ÿ�������������,���������9000Ԫ;(3)20��.
��(2)��ÿ�䷿�۶���Ϊ320Ԫʱ,����ÿ�������������,���������9000Ԫ;(3)20��.
��������
��1������ÿ���ο;�ס�ķ�����������50-���ٵķ��������ɽ�����⣮
��2���������κ��������ö��κ��������ʽ�����⣮
��3�����������г�����ʽ�鼴�ɽ�����⣮
�⣺![]() ��������,�ã�
��������,�ã�![]() ,
,![]() ,��x����
,��x����![]() ��
��![]()
![]() ,
,![]()
![]() ��
��![]() ʱ,Wȡ�����ֵ,
ʱ,Wȡ�����ֵ,![]() Ԫ,
Ԫ,
�𣺵�ÿ�䷿�۶���Ϊ320Ԫʱ,����ÿ�������������,���������9000Ԫ��
![]() ��
�� ,
,
���![]() ,
,
��![]() ʱ,���������ס���ο���������,
ʱ,���������ס���ο���������,
��������Ϊ![]() ��
��![]() ��
��


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x��1����x���һ����������Ϊ����1��0������y�ύ��Ϊ��0��3�����䲿��ͼ����ͼ��ʾ�������н��۴�����ǣ�������
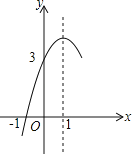
A. b![]() ��4ac��0
��4ac��0
B. ����x�ķ���ax![]() +bx+c��3��0����������ȵ�ʵ����
+bx+c��3��0����������ȵ�ʵ����
C. a��b+c��0
D. ��y��0ʱ����1��x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��湫˾���һ���ܳ�Ϊ16�ľ��ι���ƣ������Ʒ�Ϊÿƽ����2000Ԫ�������һ�߳�Ϊx�����ΪSƽ���ף�
��1����S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����Ʒ��ܴﵽ24000Ԫ��Ϊʲô��
��3����x�Ƕ�����ʱ����Ʒ���ࣿ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ͼ����C(0��-2)������D������Ϊ��1��
��ͼ����C(0��-2)������D������Ϊ��1��![]() ������
������![]() �ύ��A��B����.
�ύ��A��B����.
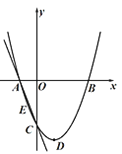
��1���������ߵĽ���ʽ.
��2������AC��EΪֱ��AC��һ�㣬����AOC�ס�AEBʱ�����E�������![]() ��ֵ.
��ֵ.
��3����F��0��![]() ����
����![]() ����һ���㣬��
����һ���㣬��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��ֵ��С.����������Сֵ.
��ֵ��С.����������Сֵ.
��4����C����![]() ��ĶԳƵ�ΪH����
��ĶԳƵ�ΪH����![]() ȡ��Сֵʱ���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��QHF��ֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵������.
ȡ��Сֵʱ���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��QHF��ֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B����ͬʱ��������ͬһ����·�ϣ�������ʻ��������У�����������ʱֹͣ.�׳���ʻһ��ʱ������ͣ��0.5Сʱ�����Ͻ��������ԭ����B����ʻ������֮���·��y��ǧ�ף������������ʱ��x(Сʱ��֮��ĺ�����ϵ��ͼ��ʾ.

��1����ס���������ʻ���ٶ�V����V��.
��2����m��ֵ.
��3�����׳�û�й���ͣ�����������ǰ�ʱ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
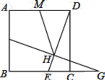
����Ŀ����ͼ���߳�Ϊ![]() ��������
��������![]() ����
����![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��һ�㣮��
��һ�㣮��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ǡ����
ǡ����![]() �ӳ����ϣ�
�ӳ����ϣ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ����
����![]() =_____��
=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����7�֣���2015��ʯ����ͼ����O��ֱ��AB=4����ABC=30����BC����O��D��D��BC���е㣮

��1����BC�ij���
��2������D��DE��AC������ΪE����֤��ֱ��DE����O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��a(x��1)2+4��ͼ����(��1��0)��
(1)��������κ����Ľ���ʽ��
(2)�ж�������κ����Ŀ��ڷ��Գ���Ͷ������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(9��)��֪��![]() ABCD������AB��AD�ij��ǹ���x�ķ���
ABCD������AB��AD�ij��ǹ���x�ķ���![]() ������ʵ������
������ʵ������
��1����mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
��2����AB�ij�Ϊ2����ô![]() ABCD���ܳ��Ƕ��٣�
ABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com