
【题目】新知学习,若一条线段把一个平面图形分成面积相等的两部分,我们把这条段线做该平面图形的二分线解决问题:
(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是_______
②如图1,已知△ABC中,AD是BC边上的中线,点E,F分别在AB,DC上,连接EF,与AD交于点G,若![]() 则EF_____(填“是”或“不是”)△ABC的一条二分线.并说明理由.
则EF_____(填“是”或“不是”)△ABC的一条二分线.并说明理由.

(2)如图2,四边形ABCD中,CD平行于AB,点G是AD的中点,射线CG交射线BA于点E,取EB的中点F,连接CF.求证:CF是四边形ABCD的二分线.

【答案】(1)①中线②是(2)证明见解析
【解析】
(1)①由平面图形的二分线定义可求解;
②由面积的和差关系可得S△BEF=S△ABD=![]() S△ABC,可得EF是△ABC的一条二分线;
S△ABC,可得EF是△ABC的一条二分线;
(2)根据EB的中点F,所以S△CBF=S△CEF,由AB∥DC,G是AD的中点,证明△CDG≌△EAG,所以S四边形AFCD=S△CEF,所以S四边形AFCD=S△CBF,可得CF是四边形ABCD的二分线;
解:(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是中线,
故答案为:中线;.
②∵AD是BC边上的中线,
∴S△ABD=S△ACD,
又∵![]() ,
,
∴S四边形BEGD=S四边形AGFC,
∴S四边形BEGD+![]() =S四边形AGFC+
=S四边形AGFC+![]() ,
,
∴![]() =S四边形AEFC,
=S四边形AEFC,
所以EF是△ABC的一条二分线,
故答案为:是;
(2)如图:
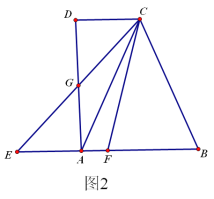
∵点G是AD的中点,
∴GD=AG,
∵AB∥DC,
∴∠D=∠GAE,
在△CDG和△EAG中,
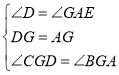 ,
,
∴△CDG≌△EAG(ASA),
∴S△CDG=S△EAG,
∵点F是EB的中点,
∴S△CFE=S△CBF,
即S△AGE+S四边形AGCF=S△CBF,
∴S△CDG+S四边形AGCF=S△CBF,即S四边形ADCF=S△CBF,
∴CF是四边形ABCD的二分线;


科目:初中数学 来源: 题型:
【题目】数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
(1) (思想应用)已知m, n均为正实数,且m+n=2求![]() 的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
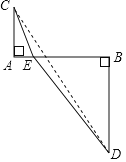
①用含m的代数式表示CE=_______, 用含n的代数式表示DE= ;
②据此求![]() 的最小值;
的最小值;
(2)(类比应用)根据上述的方法,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度Vl与V2(Vl<V2),甲用一半的路程使用速度Vl、另一半的路程使用速度V2;乙用一半的时间使用速度Vl、另一半的时间使用速度V2;关于甲乙二人从A地到达B地的路程与时间的函数图象及关系,有图中4个不同的图示分析.其中横轴t表示时间,纵轴s表示路程,其中正确的图示分析为( )

A. 图(1) B. 图(1)或图(2) C. 图(3) D. 图(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
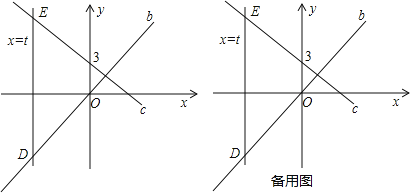
【题目】如图,已知直线c和直线b相较于点![]() ,直线c过点
,直线c过点![]() 平行于y轴的动直线a的解析式为
平行于y轴的动直线a的解析式为![]() ,且动直线a分别交直线b、c于点D、
,且动直线a分别交直线b、c于点D、![]() 在D的上方
在D的上方![]() .
.
![]() 求直线b和直线c的解析式;
求直线b和直线c的解析式;
![]() 若P是y轴上一个动点,且满足
若P是y轴上一个动点,且满足![]() 是等腰直角三角形,求点P的坐标.
是等腰直角三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列几个命题中正确的个数为 个.
①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4,5,6).
②5名同学的语文成绩为90,92,92,98,103,则他们平均分为95,众数为92.
③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定.
④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清楚数据,所以对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.
个人年创利润/万元 | 10 | 8 | 5 | 3 |
员工人数 | 1 | 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3 m,BC=4 m,CD=12 m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米30元,试问铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个圆柱形玻璃杯高![]() ,底面周长为
,底面周长为![]() ,有一只蚂蚁在一侧距下底
,有一只蚂蚁在一侧距下底![]() 的外侧
的外侧![]() 点,与点
点,与点![]() 正对的容器内侧距下底
正对的容器内侧距下底![]() 的
的![]() 点处有一饭粒,蚂蚁想吃
点处有一饭粒,蚂蚁想吃![]() 处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________
处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(1)写出△ABC的各顶点坐标;
(2)画出△ABC关于y轴的对称图形△A1B1C1;
(3)写出△ABC关于x轴对称的三角形的各顶点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com