
【题目】如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An﹣1为OA的n等分点,B1、B2、B3、…Bn﹣1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An﹣1Bn﹣1 , 分别交![]() (x≥0)于点C1、C2、C3、…、Cn﹣1 , 当B25C25=8C25A25时,则n= .
(x≥0)于点C1、C2、C3、…、Cn﹣1 , 当B25C25=8C25A25时,则n= . 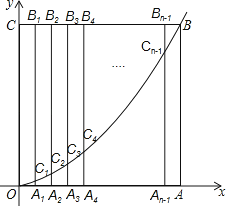
【答案】75
【解析】解:∵正方形OABC的边长为n,点A1 , A2 , …,An﹣1为OA的n等分点,点B1 , B2 , …,Bn﹣1为CB的n等分点,
∴OA25=![]() n=25,A25B25=n,
n=25,A25B25=n,
∵B25C25=8C25A25 ,
∴C25(25,![]() ),
),
∵点C25在y=![]() x2(x≥0)上,
x2(x≥0)上,
∴![]() =
=![]() ×(25)2 ,
×(25)2 ,
解得n=75.
所以答案是:75.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,点M运动的路径长为 . 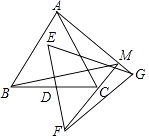
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y= ![]() x+1与x轴交于点A,且与双曲线y=
x+1与x轴交于点A,且与双曲线y= ![]() 的一个交点为B(
的一个交点为B( ![]() ,m).
,m).
(1)求点A的坐标和双曲线y= ![]() 的表达式;
的表达式;
(2)若BC∥y轴,且点C到直线y= ![]() x+1的距离为2,求点C的纵坐标.
x+1的距离为2,求点C的纵坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=![]() ,AC=8,求图中阴影部分的面积;
,AC=8,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )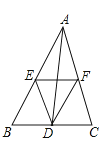
A.DE=DF
B.EF=![]() ?AB
?AB
C.S△ABD=S△ACD
D.AD平分∠BAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90°,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.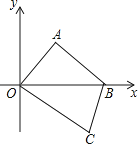
(1)求点A和点C的坐标;
(2)当0<t<30时,求m关于t的函数关系式;
(3)当m=35时,请直接写出t的值;
(4)直线l上有一点M,当∠PMB+∠POC=90°,且△PMB的周长为60时,请直接写出满足条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com