
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�Ķ���O������ԭ�㣬��A�ڵ�һ���ޣ���C�ڵ������ޣ���B������Ϊ��60��0����OA=AB����OAB=90�㣬OC=50����P���߶�OB�ϵ�һ�����㣨��P�����O��B�غϣ�������P��y��ƽ�е�ֱ��l����OA���AB�ڵ�Q������OC���BC�ڵ�R�����P������Ϊt���߶�QR�ij���Ϊm����֪t=40ʱ��ֱ��lǡ�þ�����C��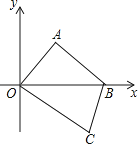
��1�����A�͵�C�����ꣻ
��2����0��t��30ʱ����m����t�ĺ�����ϵʽ��
��3����m=35ʱ����ֱ��д��t��ֵ��
��4��ֱ��l����һ��M������PMB+��POC=90�㣬�ҡ�PMB���ܳ�Ϊ60ʱ����ֱ��д�����������ĵ�M�����꣮
���𰸡�
��1��
�⣺��ͼ1������A��AD��OB������ΪD������C��CE��OB������ΪE��
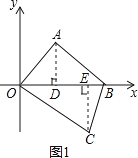
��OA=AB��
��OD=DB=![]() OB��
OB��
�ߡ�OAB=90�㣬
��AD=![]() OB��
OB��
�ߵ�B������Ϊ����60��0����
��OB=60��
��OD=![]() OB=
OB=![]() ��60=30��
��60=30��
���A����������30��30����
��ֱ��lƽ����y���ҵ�t=40ʱ��ֱ��lǡ�ù���C��
��OE=40��
��Rt��OCE��OC=50��
�ɹ��ɶ����ã�
CE=![]() =
=![]() =30��
=30��
���C����������40����30����
��2��
�⣺��ͼ2��
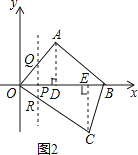
�ߡ�OAB=90�㣬OA=AB��
���AOB=45�㣬
��ֱ��lƽ����y�ᣬ
���OPQ=90�㣬
���OQP=45�㣬
��OP=QP��
�ߵ�P�ĺ�����Ϊt��
��OP=QP=t��
��Rt��OCE��
OE=40��CE=30��
��tan��EOC=![]() ��
��
��tan��POR=![]() =
=![]() ��
��
��PR=OPtan��POR=![]() t��
t��
��QR=QP+PR=t+![]() t=
t=![]() t��
t��
�൱0��t��30ʱ��m����t�ĺ�����ϵʽΪ��m=![]() t��
t��
��3��
�⣺�ɣ�2���ã���0��t��30ʱ��m=35=![]() t����ã�t=20��
t����ã�t=20��
��ͼ3��
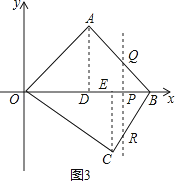
��30��t��40ʱ��m=35��Ȼ�����ܣ�
��40��t��60ʱ����OP=t����BP=QP=60��t��
��PR��CE��
���BPR�ס�BEC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��ã�PR=90��![]() t��
t��
��m=60��t+90��![]() t=35��
t=35��
��ã�t=46��
����������t��ֵΪ20��46��
��4��
�⣺��ͼ4��
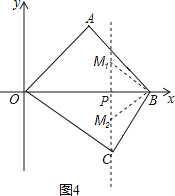
����PMB+��POC=90���ҡ�PMB���ܳ�Ϊ60ʱ����ʱt=40��ֱ��lǡ�þ�����C��
���MBP=��COP��
�ʴ�ʱ��BMP�ס�OCP��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��ã�x=15��
��M1��40��15����ͬ���ɵã�M2��40����15����
������������������ĵ������Ϊ��M1��40��15����M2��40����15����
����������1�����õ��������ε������Լ����ɶ������B������ó�A��C�����ꣻ
��2������������Ǻ�����ϵ��ϣ�1��������ó�PR��QP�ij�������������ɣ�
��3�����ã�2�����������õ�0��t��30ʱ����30��t��60ʱ���ֱ�����m��t�Ĺ�ϵʽ������ɣ�
��4���������������ε����ʣ��ó�M�����꼴�ɣ�
�����㾫�����������⣬������Ҫ�˽����������ε��ж�������(���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��)��


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У�BC���ϵĸ�Ϊ4��AB=5��AC=2 ![]() ����ƽ���ı���ABCD���ܳ����� ��
����ƽ���ı���ABCD���ܳ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊn��������OABC�ı�OA��OC�ֱ���x���y����������ϣ�A1��A2��A3������An��1ΪOA��n�ȷֵ㣬B1��B2��B3����Bn��1ΪCB��n�ȷֵ㣬����A1B1��A2B2��A3B3������An��1Bn��1 �� �ֱ�![]() ��x��0���ڵ�C1��C2��C3������Cn��1 �� ��B25C25=8C25A25ʱ����n= ��
��x��0���ڵ�C1��C2��C3������Cn��1 �� ��B25C25=8C25A25ʱ����n= �� 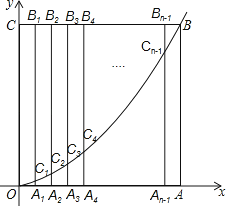
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AD��BC���ϵ����ߣ���ADΪֱ������O������BO���ӳ���E��ʹ��OE=OB������AE��
��1����֤��AE�ǡ�O�����ߣ�
��2����BD=![]() AD=4������Ӱ���ֵ������
AD=4������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��
��EΪ����ABCD��һ�㣬AE=DE������EB��EC�ֱ���AD�ཻ�ڵ�F��G����֤��
��1����EAB�ա�EDC��
��2����EFG=��EGF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c=��a��0��ͼ���һ���֣��Գ�����ֱ��x=��2���������н��ۣ���ab��0����b2��4ac��0����9a��3b+c��0����b��4a=0���ݷ���ax2+bx=0��������Ϊx1=0��x2=��4��������ȷ�Ľ����У�������
A.�٢ۢ�
B.�ڢܢ�
C.�٢ڢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ֧Ԯ������ijУ���ĻС�����óO���ʽ���A��B�����ͺŵ�ѧϰ��Ʒ��1000������֪B��ѧϰ��Ʒ�ĵ��۱�A��ѧϰ��Ʒ�ĵ��۶�10Ԫ����180Ԫ����B��ѧϰ��Ʒ�ļ�������120Ԫ����A��ѧϰ��Ʒ�ļ�����ͬ��
��1����A��B����ѧϰ��Ʒ�ĵ��۸��Ƕ���Ԫ��
��2������������ѧϰ��Ʒ�ķ��ò�����28000Ԫ��������B��ѧϰ��Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A�ڵ�һ���ޣ���A��x�ύ��B��2��0����C��8��0�����㣬��y�������ڵ�D�����A�������ǣ�������
A.��5��4��
B.��4��5��
C.��5��3��
D.��3��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��������ABCD�ڵ�һ�㣬����CP�����߶�CP�Ƶ�C˳ʱ����ת90�㣬�õ��߶�CQ������BP��DQ��
��1����ͼa����֤����BCP�ա�DCQ��
��2����ͼ���ӳ�BP��ֱ��DQ�ڵ�E��
����ͼb����֤��BE��DQ��
����ͼc������BCPΪ�ȱ������Σ��жϡ�DEP����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com