
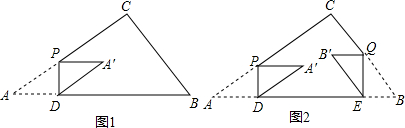
分析 (1)①旋转变换中,对应的边相等,再根据“两组对边分别相等”,则可判断出ADA'P为平行四边形,②当A’在BC边上时,根据线段之间的数量关系,求出x的值;
(2)分两种情况讨论,①当A'在△ABC的内部和边BC上,②当A'在△ABC的外部,两种情况分别用x表示相应线段的长度,则可求得y与x的函数关系式;
(3)由A'B'⊥AB,分析得到题中隐藏的相等线段,即可求得A'B'的长度.
解答 解:(1)①如图1,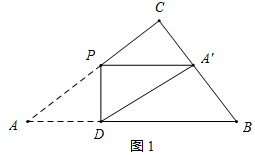
由旋转的性质可知:PA'=AD,PA=A'D,
故答案为:平行四边形;
②由AB2=AC2+BC2,得AB=$\sqrt{41}$,
∵sin∠A=$\frac{BC}{AB}=\frac{4}{\sqrt{41}}$,cos∠A=$\frac{AC}{AB}=\frac{5}{\sqrt{41}}$,AP=5x,
∴PA'=AD=APcos∠A=$\frac{25x}{\sqrt{41}}$,CP=5-5x,
∵cos∠CPA'=cos∠A=$\frac{CP}{PA′}$,即$\frac{5-5x}{\frac{25x}{\sqrt{41}}}$=$\frac{5}{\sqrt{41}}$,
解得x=$\frac{41}{66}$;
(2)如图2,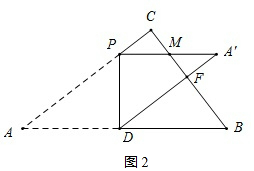
①当0<x≤$\frac{41}{66}$时,
∵A'P=AD=AP cos∠A=$\frac{25x}{\sqrt{41}}$,PD=APsin∠A=$\frac{20x}{\sqrt{41}}$,A'D=AP=5x,
∴y=A'P+PD+A'D=$\frac{25x}{\sqrt{41}}+\frac{20x}{\sqrt{41}}+5x=\frac{45\sqrt{41}+205}{41}x$;
②当$\frac{41}{66}$<x≤1时,
∵PM=$\frac{PC}{cos∠A}=\sqrt{41}(1-x)$,
DF=DBcosA=$\frac{41-25x}{\sqrt{41}}•\frac{5\sqrt{41}}{41}=\frac{205-125x}{41}$,
∴y=PM+PD+DF=$\sqrt{41}(1-x)+\frac{20x}{\sqrt{41}}+\frac{205-125x}{41}=\frac{(20\sqrt{41}-166)x+246}{41}$;
(3)如图3,设B'A'垂直AB于H,
则DH=PA'=AD,HE=B'Q=EB,
∴AB=2AD+2EB,即2×$\frac{25x}{\sqrt{41}}$+2×$\frac{20x}{\sqrt{41}}$=$\sqrt{41}$,
解得:x=$\frac{41}{90}$,
又∵B′H=QE=BQsinB=5x•$\frac{5}{\sqrt{41}}$=$\frac{25x}{\sqrt{41}}$,A′H=PD=APsinA=5x•$\frac{4}{\sqrt{41}}$=$\frac{20x}{\sqrt{41}}$,
∴A'B'=B'H-A'H=$\frac{5x}{\sqrt{41}}$=$\frac{5}{\sqrt{41}}$×$\frac{41}{90}$=$\frac{\sqrt{41}}{18}$,
∴A'B'的长度为$\frac{\sqrt{41}}{18}$.
点评 此题考查了旋转变换的性质、平行四边形的判定、分类讨论思想的运用,熟练掌握平行四边形的判定及解直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
| 年龄x/岁 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 身高h/cm | 48 | 100 | 130 | 140 | 150 | 158 | 165 | 170 | 170.4 |
| A. | 赵先生的身高增长速度总体上先快后慢 | |
| B. | 赵先生的身高在21岁以后基本不长了 | |
| C. | 赵先生的身高从0岁到12岁平均每年增高12.5cm | |
| D. | 赵先生的身高从0岁到24岁平均每年增高5.1cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 26cm | B. | 52cm | C. | 78cm | D. | 104cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com