
分析 本题可设鸡有x只,兔有y只,因“今有雉(鸡)兔同笼,上有三十五头,下有九十四足.”,所以有$\left\{\begin{array}{l}{x+y=35}\\{2x+4y=94}\end{array}\right.$,解之得鸡的只数,兔的只数.
解答 解:设鸡有x只,兔有y只,根据题意得
有$\left\{\begin{array}{l}{x+y=35}\\{2x+4y=94}\end{array}\right.$,
解之,得$\left\{\begin{array}{l}{x=23}\\{y=12}\end{array}\right.$,
即有鸡23只,兔12只.
点评 本题考查了二元一次方程组的应用.注意:每只兔子有4只足,每只鸡有2只足.解题关键是弄清题意,合适的等量关系,列出方程组.


科目:初中数学 来源: 题型:选择题
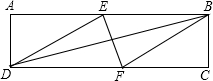 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:| A. | ①正确,②正确 | B. | ①正确,②错误 | C. | ①错误,②正确 | D. | ①错误,②错误 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
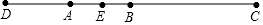 已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.
已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 污水处理器型号 | A型 | B型 |
| 处理污水能力(吨/月) | 240 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
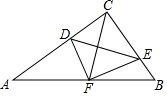 如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$.
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com