
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1. 
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.
【答案】
(1)解:由题意得:
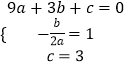 ,
,
解该方程组得:a=﹣1,b=2,c=3,
∴抛物线的解析式为y=﹣x2+2x+3
(2)解:由题意得:OA=3,OB=3;
由勾股定理得:AB2=32+32,
∴AB=3 ![]() .
.
当△ABM为等腰三角形时,
①若AB为底,
∵OA=OB,
∴此时点O即为所求的点M,
故点M的坐标为M(0,0);
②若AB为腰,
以点B为圆心,以3 ![]() 长为半径画弧,交y轴于两点,
长为半径画弧,交y轴于两点,
此时两点坐标为M(0,3﹣3 ![]() )或M(0,3+3
)或M(0,3+3 ![]() ),
),
以点A为圆心,以3 ![]() 长为半径画弧,交y轴于点(0,﹣3);
长为半径画弧,交y轴于点(0,﹣3);
综上所述,当△ABM为等腰三角形时,点M的坐标分别为
(0,0)、(0,3﹣3 ![]() )、(0,3
)、(0,3 ![]() +3)、(0,﹣3).
+3)、(0,﹣3).
【解析】(1)直接根据题意列出关于a、b、c的方程组,解方程组即可解决问题.(2)运用分类讨论的数学思想,根据等腰三角形的定义,分类讨论,数形结合,即可解决问题.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
①△ABE≌△DCF;② ![]() ;③DP2=PHPB;④
;③DP2=PHPB;④ ![]() .
.
其中正确的是 . (写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有一个呈等腰直角三角形的积木盒,现在积木盒中只剩下如图1所示的九个空格,图2是可供选择的A,B,C,D四块积木. 
(1)小明选择把积木A和B放入图3,要求积木A和B的九个小圆恰好能分别与图3中的九个小圆重合,请在图3中画出他放入方式的示意图(温馨提醒:积木A和B的连接小圆的小线段还是要画上哦!);
(2)现从A、B、C、D四块积木中任选两块,请用列表法或画树状图法求恰好能全部不重叠放入的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列命题的已知、求证,并完成证明过程.
命题:如果一个三角形的两条边相等,那么两条边所对的角也相等(简称:“等边对等角”.)
(1)已知: .
求证: .
(2)证明:“等边对等角”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com