
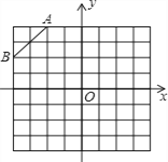
����Ŀ����ͼ�ǹ��Ϊ8��8��������������������������������Ҫ�������
��1���ڵڶ������ڵĸ������һ��C�� ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ� ���������������� ��C��������____________����ABC�������_____________________��
��2��������ABC���Ե�CΪ��ת���ġ���ת180������A��B��C������AB����A��B�� ���ı���AB A��B������״�Ǻ������ı��Σ�___________________��
��3�������������Ƿ����P�㣬ʹ�á�PAB���CAB�������ȣ������ڣ���ֱ��д����P�����꣨д��һ��������ɣ�___________________��
���𰸡� C��-1,1�� 4 ���� P��0,2����-2,0��
����������������1��������������ѡ�ɣ��𰸲�Ψһ�������ù��ɶ�������֤����Ϊ���������ø�������ABC�������
��2��������ת180������ԭͼ�γ����ĶԳƣ������ӳ�AC��BD��ʹ![]() ,
,![]() ,���ɻ���ͼ�Σ�Ȼ����ݾ��ε��ж�����˵�����ɣ�
,���ɻ���ͼ�Σ�Ȼ����ݾ��ε��ж�����˵�����ɣ�
��3��������������ѡ��Ȼ����������֤.
��⣺��1����ͼ��ȡ��C��-1,1������AC=BC=![]() ��
��
��ABC�����=4��4-![]() ��
��
��2���ӳ�AC��BD��ʹ![]() ,
,![]() ������AB����A��B��B���B��
������AB����A��B��B���B��
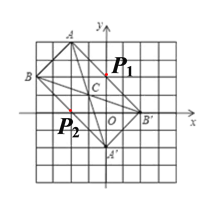
�������֪��BC=CB�䣬AC=CA�䣬
���ı���ABA��B����ƽ���ı��Σ�
�֡�AA��=BB�䣬
���ı���ABA��B���Ǿ�����
��3����ͼ����P1��0,2��ʱ��
S��ABP1=![]() ,�������⣻
,�������⣻
��P2��-2,0��ʱ��
S��ABP1=![]() ,�������⣻
,�������⣻
��P�������ǣ�0,2����-2,0��.


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����ABC�У���C=90�㣬AB�Ĵ�ֱƽ���߽�AC�ڵ�D������BD����AC=2��BC=1�����BCD���ܳ�Ϊ��
��2��OΪ������ABCD�����ģ�EΪCD����һ�㣬FΪAD����һ�㣬�ҡ�EDF���ܳ�����AD�ij���
����ͼ2��������EDF��Ҫ�߹���ͼ����д������������ͼ�ۼ�����
����ͼ3�в�ȫͼ�Σ����EOF�Ķ�����
����![]() �� ��
�� ��![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��ͼ�ξ��۵����γ���ͼ����ʾ��������

![]() ��������м������棿�����������������ʲô��ϵ��
��������м������棿�����������������ʲô��ϵ��
![]() ͼ������Щͼ�ε���״���Сһ����ȫ��ͬ��
ͼ������Щͼ�ε���״���Сһ����ȫ��ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ�ֱ��![]() ��
��![]() ��
��![]() �ֱ�ͨ��A��B��C���㣬��
�ֱ�ͨ��A��B��C���㣬��![]() ����
����![]() ��
��![]() �ľ���Ϊ5��
�ľ���Ϊ5��![]() ��
��![]() �ľ���Ϊ7����������ABCD���������( )
�ľ���Ϊ7����������ABCD���������( )

A. 148 B. 70 C. 144 D. 74
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ���и���P(1��0)����P��1����������1����λ����P1(1��1)�������ŵ�2����������2����λ����P2(�D1��1)����3����������1����λ����4����������3����λ����5������������1����λ����6����������4����λ�����������˹���������ȥ����P��100����������P100�������� ��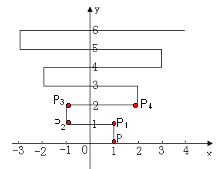
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��E�ֱ���AC��DF�ϣ�AF�ֱ�BD��CE�ڵ�M��N����A=��F����1=��2��
��1����֤���ı���BCED��ƽ���ı��Σ�
��2����֪DE=2������BN����BNƽ����DBC����CN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����й����廪��ѧ��������ѧ��Ӣ���Ľ��Ŵ�ѧ��ͼƬ�ֱ�����3����ȫ��ͬ�IJ�����Ӳֽ���ϣ��Ƴ���У��Ƭ����ͼ��С������3�ſ�Ƭ���泯��ϴ�Ⱥ���������ϣ��������ȡһ�ſ�Ƭ���Żغ�ϴ�ȣ��������ȡһ�ſ�Ƭ��
��1��С����һ�γ�ȡ�Ŀ�Ƭ�ϵ�ͼƬ�ǽ��Ŵ�ѧ�ĸ����Ƕ��٣�����ֱ��д�������
��2���������б�������״ͼ����״ͼ����������С��������γ�ȡ�Ŀ�Ƭ�ϵ�ͼƬһ���ǹ��ڴ�ѧ��һ���ǹ����ѧ�ĸ��ʣ�����Ƭ���ƿ�����ĸ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ֱ֪��y=��2x+4����������ֱ��ڵ�A��B����CΪ�߶�OA��һ���㣬����BC����BC���д��߷ֱ�OB��AB���ڵ�D��E��
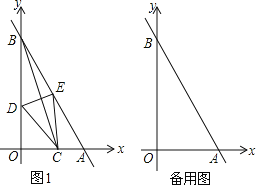
��l������C���O�غ�ʱ��DE= ��
��2����CE��OBʱ��֤����ʱ�ı���BDCEΪ���Σ�
��3���ڵ�C���˶������У�ֱ��д��OD��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������߳���Ϊ2�������ΰ���ͼ��ʾ�ڷţ���A1��A2��A3��A4�ֱ����ĸ������ε����ģ���ͼ���Ŀ���Ӱ���ֵ�����ĺ�Ϊ______��
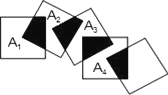
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com