
【题目】某商贩出售一批进价为l元的钥匙扣,在销售过程中发现钥匙扣的日销售单价x(元)与日销售量y(个)之间有如下关系:

(1)根据表中数据在平面直角坐标系中,描出实数对(x,y)对应的点;
(2)猜想并确定y与x的关系式,并在直角坐标系中画出x>0时的图像;
(3)设销售钥匙扣的利润为T元,试求出T与x之间的函数关系式:若商贩在钥匙扣售价不超过8元的前提下要获得最大利润,试求销售价x和最大利润T.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,4),B(4,0),分别将点A、B的横坐标、纵坐标都乘以1.5,得相应的点A'、B'的坐标。

(1)画出 OA'B':
(2)△OA'B'与△AOB______位似图形:(填“是”或“不是”)
(3)若线段AB上有一点![]() ,按上述变换后对应的A'B'上点的坐标是______.
,按上述变换后对应的A'B'上点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
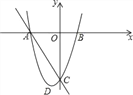
【题目】如图,抛物线的图象与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,点D是抛物线的顶点,且A(﹣6,0),D(﹣2,﹣8).
(1)求抛物线的解析式;
(2)点P是直线AC下方的抛物线上一动点,不与点A、C重合,求过点P作x轴的垂线交于AC于点E,求线段PE的最大值及P点坐标;
(3)在抛物线的对称轴上足否存在点M,使得△ACM为直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过原点O及点A
经过原点O及点A![]() 和点B
和点B![]() .
.
(1)求抛物线的解析式;
(2)如图1,设抛物线的对称轴与x轴交于点C,将直线![]() 沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;
沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;
(3)如图2,将抛物线向上平移9个单位得到新抛物线,直接写出下列两个问题的答案:
①直线![]() 至少向上平移多少个单位才能与新抛物线有交点?
至少向上平移多少个单位才能与新抛物线有交点?
②新抛物线上的动点Q到直线![]() 的最短距离是多少?
的最短距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一拱桥的截面呈抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,拱桥与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m景观灯.
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com