
【题目】如图,在平面直角坐标系中,点A(-4,0),点B(0,-5),点C(m,0)(m>0),过点A作直线BC的垂线交y轴于点D,则随着m值的增大,经过A,D,C三点的抛物线的开口大小的变化情况是( )
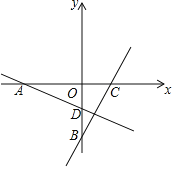
A.保持不变B.逐渐变大C.逐渐变小D.时大时小
【答案】A
【解析】
设OD=n,首先易证△OAD∽△OBC,列出比例式求出n=![]() ,即可得到点D坐标,然后设经过A,D,C三点的抛物线的解析式为y=a(x+4)(x﹣m),将点D坐标代入可求出a=
,即可得到点D坐标,然后设经过A,D,C三点的抛物线的解析式为y=a(x+4)(x﹣m),将点D坐标代入可求出a=![]() ,问题得解.
,问题得解.
设OD=n,
∵点A(﹣4,0),点B(0,﹣5).点C(m,0)(m>0),
∴OA=4,OB=5,OC=m,
∵AD⊥BC,
∴∠OAD=∠DBC,
∴△OAD∽△OBC,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴n=![]() ,
,
∴D(0,![]() ),
),
设经过A,D,C三点的抛物线的解析式为y=a(x+4)(x﹣m),
将D(0,![]() )代入可得:
)代入可得:![]() =﹣4ma,
=﹣4ma,
∴a=![]() ,
,
∴抛物线对的解析式为:y=![]() (x+4)(x﹣m),
(x+4)(x﹣m),
由于抛物线的二次项系数为![]() ,
,
∴经过A,D,C三点的抛物线的开口大小不变,
故选:A.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是一元二次方程(a-6)x2+2ax+a=0的两个实数根.
(1)求实数a的取值范围;
(2)若x1、x2满足x1x2-x1=4+ x2,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了46米木栏.
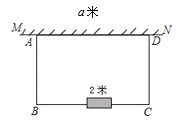
(1)若a=26,所围成的矩形菜园的面积为280平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:

(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个足球垂直地面向上踢,![]() (秒)后该足球的高度
(秒)后该足球的高度![]() (米)适用公式
(米)适用公式![]() .
.
(1)经多少秒时足球的高度为20米?
(2)小明同学说:“足球高度不可能达到21米!”你认为他说得对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
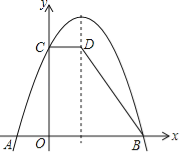
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-![]() .
.
(1)将y=-![]() +x+
+x+![]() 用配方法化为y=a(x-h)2+k的形式;
用配方法化为y=a(x-h)2+k的形式;
(2)求该函数图象与两坐标轴交点的坐标;
(3)画出该函数的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com