练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在四边形ABCD中，AD∥BC， ，点E是BC的中点，连接AE、BD．若EA⊥AB，BC＝26，DC＝12，求△ABD的面积.

    【答案】解：连接DE，

    ∵点E是BC的中点，BC=26，
    ∴BE=EC= BC=13，
    ∵AD= BC，
    ∴AD=BE=CE=13．
    ∵AD∥BE，
    ∴四边形ABED与四边形AECD都是平行四边形，
    ∴AE=DC=12，S△ABD= SABED ．
    在△ABE中，
    ∵∠BAE=90°，
    ∴AB= ，
    ∴S△ABD= SABED= ×5×12=30．
    【解析】连接DE，根据点E是BC的中点，AD= BC，可得出四边形ABED与四边形AECD都是平行四边形，故可得出AE=DC=12，S△ABD= SABED ， 根据勾股定理求出AB的长，进而可得出结论。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知m+n=3，m﹣n=2，那么m2﹣n2的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因式分解

    （1）x2-9y2

    （2）2x2y-8xy+8y

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】a5可以等于（　　）

    A.（﹣a）2（﹣a）3B.（﹣a）（﹣a）4

    C.（﹣a2）a3D.（﹣a3）（﹣a2）

    查看答案和解析>>

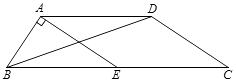
    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，直线l1：y=x与直线l2：y=﹣x+6交于点A，l2与x轴交于B，与y轴交于点C．

    （1）求△OAC的面积；

    （2）如点M在直线l2上，且使得△OAM的面积是△OAC面积的，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a+b=2，ab=-1，求下面代数式的值：

    （1）a2+b2；（2）（a-b）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a<b，则下列各式中正确的是（ ）

    A.a<-bB.a-3<a-8C.a2<b2D.-3a>-3b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题背景

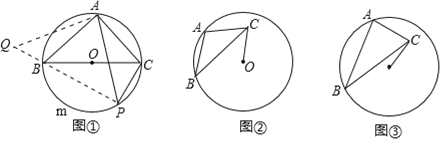
    如图①，BC是⊙O的直径，点A在⊙O上，AB=AC，P为BmC上一动点（不与B，C重合），求证： PA=PB+PC．

    小明同学观察到图中自点A出发有三条线段AB，AP，AC，且AB=AC，这就为旋转作了铺垫．于是，小明同学有如下思考过程：

    第一步：将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；

    第二步：证明Q，B，P三点共线，进而原题得证．

    请你根据小明同学的思考过程完成证明过程．

    （2）类比迁移

    如图②，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=AC，AB⊥AC，垂足为A，求OC的最小值．

    （3）拓展延伸

    如图③，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=AC，AB⊥AC，垂足为A，则OC的最小值为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题发现：

    （）如图①，中，，，，点是边上任意一点，则的最小值为__________．

    （）如图②，矩形中，，，点、点分别在、上，求的最小值．

    （）如图③，矩形中，，，点是边上一点，且，点是边上的任意一点，把沿翻折，点的对应点为点，连接、，四边形的面积是否存在最小值，若存在，求这个最小值及此时的长度；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案