
如图,在平面直角坐标系xOy中,点A( ,0),点B(0,2),点C是线段OA的中点.
,0),点B(0,2),点C是线段OA的中点.
(1)点P是直线AB上的一个动点,当PC+PO的值最小时,
①画出符合要求的点P(保留作图痕迹);
②求出点P的坐标及PC+PO的最小值;
(2)当经过点O、C的抛物线y=ax2+bx+c与直线AB只有一个公共点时,求a的值并指出这个公共点所在象限.

(1)①作图见解析;②(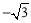 ,1);(2)当
,1);(2)当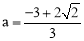 时,公共点在第三象限, 当
时,公共点在第三象限, 当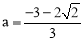 时,公共点在第二象限.
时,公共点在第二象限.
【解析】
试题分析:(1)①根据轴对称的性质,作点C关于直线AB的对称点D,连接OD,OD与直线AB的交点P 即为所求.
②应用待定系数法求出直线AB和直线OD的表达式,联立二者即为所求.
(2)根据抛物线y=ax2+bx+c经过点O、C,得出解析式为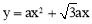 ,根据抛物线
,根据抛物线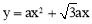 与直线
与直线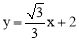 只有一个公共点得到
只有一个公共点得到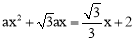 的根的差别式等于0,从而求得a的值,进而求得交点坐标,判断出其所在象限.
的根的差别式等于0,从而求得a的值,进而求得交点坐标,判断出其所在象限.
(1)①如图1.
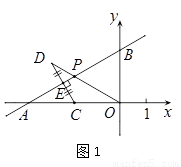
②如图2,作DF⊥OA于点F,根据题意,得AC=CO=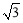 ,∠BAO=30°,CE=DE,
,∠BAO=30°,CE=DE,
∴ CD=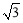 ,CF=
,CF=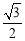 ,DF=
,DF=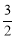 .∴ D(
.∴ D(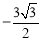 ,
,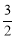 ).
).
求得直线AB的表达式为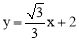 ,直线OD的表达式为
,直线OD的表达式为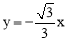 ,
,
∴ P(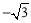 ,1).
,1).
在△DFO中,可求得 DO=3.∴PC+PO的最小值为3.

(2)∵抛物线y=ax2+bx+c经过点O、C,
∴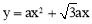 .
.
由题意,得 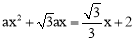 .
.
整理,得 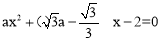 .
.
∵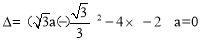 .∴
.∴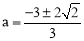 .
.
当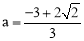 时,公共点在第三象限, 当
时,公共点在第三象限, 当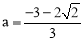 时,公共点在第二象限.
时,公共点在第二象限.
考点:1.一次函数和二次函数综合题;2.动点问题;3.轴对称的应用(最短线路问题);4.待定系数法的应用,5.曲线上点的坐标与方程的关系;6.含30度角直角三角形的性质;7.一元二次方程根的判别式的应用;8.平面直角坐标系中各象限点的特征.


科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
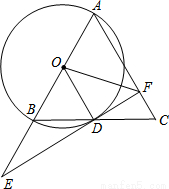
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.
(1)求证:OD∥AC;
(2)当AB=10,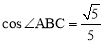 时,求AF及BE的长.
时,求AF及BE的长.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:选择题
小月的讲义夹里放了大小相同的试卷共12页,其中语文5页、数学4页、英语3页,她随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率是( )
A.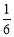 B.
B.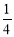 C.
C.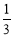 D.
D.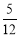
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:解答题
在一次数学游戏中,老师在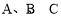 三个盘子里分别放了一些糖果,糖果数依次为
三个盘子里分别放了一些糖果,糖果数依次为 ,
,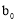 ,
, ,记为
,记为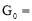 (
( ,
,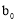 ,
, ).游戏规则如下: 若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作. 若三个盘子中的糖果数都相同,游戏结束.
).游戏规则如下: 若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作. 若三个盘子中的糖果数都相同,游戏结束.  次操作后的糖果数记为
次操作后的糖果数记为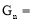 (
( ,
,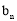 ,
,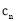 ).
).
(1)若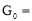 (4,7,10),则第_______次操作后游戏结束;
(4,7,10),则第_______次操作后游戏结束;
(2)小明发现:若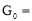 (4,8,18),则游戏永远无法结束,那么
(4,8,18),则游戏永远无法结束,那么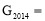 ________.
________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:选择题
如图,AB为⊙O的弦,OC⊥AB于C,AB=8,OC=3,则⊙O的半径长为( )

A. B.3 C.4 D.5
B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:解答题
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.以下是相关的统计图、表:

(1)请根据所给信息补全扇形统计图;
(2)请你根据“2013年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2013年机动车保有量已突破520万辆,请你通过计算,估计2013年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB , CD
, CD

【小题1】求作此残片所在的圆(不写作法,保留作图痕迹)
【小题2】求(1)中所作圆的半径
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com