
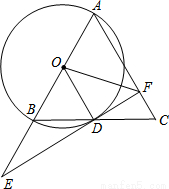
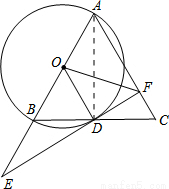
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.
(1)求证:OD∥AC;
(2)当AB=10,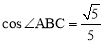 时,求AF及BE的长.
时,求AF及BE的长.
(1)证明见解析;(2)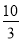 .
.
【解析】
试题分析:(1)若要证明OD∥AC,则可转化为证明∠C=∠ODB即可.
(2)连接AD,首先利用已知条件可求出BD的长,再证明△ADC∽△AFD,利用相似三角形的性质:对应边的比值相等即可求出AF及BE的长.
试题解析:(1)∵AB=AC,∴∠ABC=∠C.
∵OB=OD,∴∠OBD=∠ODB.∴∠C=∠ODB.
∴OD∥AC.
(2)如图,连接AD,
∵AB为直径,∴AB⊥BD.∴∠ADC=90°.
∵AB=10,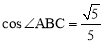 ,∴BD=AB•cos∠ABC=
,∴BD=AB•cos∠ABC=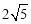 .∴AD=
.∴AD=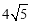 .
.
∵DF是圆的切线,∴OD⊥DF.∴∠ODF=90°.
∵AC∥OD,∴∠AFD=90°.
∵∠ADC=∠AFD,∠DAF=∠CAD,∴△ADC∽△AFD,
∴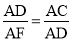 ,即
,即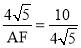 ,解得AF=8.
,解得AF=8.
∵OD∥AF,∴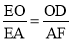 ,即
,即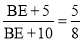 .
.
∴BE=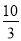 .
.
考点:1.切线的性质;2.相似三角形的判定和性质;3.平行线的判定和性质;4.圆周角定理.


科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:填空题
以下四个命题:
①每一条对角线都平分一组对角的平行四边形是菱形.
②当m > 0时, y =–mx+1与 两个函数都是y随着x的增大而减小.
两个函数都是y随着x的增大而减小.
③已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若A点坐标为(1, )则D点坐标为(1,
)则D点坐标为(1, ).
).
④在一个不透明的袋子中装有标号为1,2,3,4的四个完全相同的小球,从袋中随机摸取一个然后放回,再从袋中随机地摸取一个,则两次取到的小球标号的和等于4的概率为 .
.
其中正确的命题有 (只需填正确命题的序号)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市通州区中考二模数学试卷(解析版) 题型:选择题
对于实数 ,我们规定
,我们规定 表示不大于
表示不大于 的最大整数,例如
的最大整数,例如 ,
, ,
, .若
.若 ,则
,则 的取值可以是( )
的取值可以是( )
A.40 B.45 C.51 D.56
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,点A( ,0),点B(0,2),点C是线段OA的中点.
,0),点B(0,2),点C是线段OA的中点.
(1)点P是直线AB上的一个动点,当PC+PO的值最小时,
①画出符合要求的点P(保留作图痕迹);
②求出点P的坐标及PC+PO的最小值;
(2)当经过点O、C的抛物线y=ax2+bx+c与直线AB只有一个公共点时,求a的值并指出这个公共点所在象限.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com