
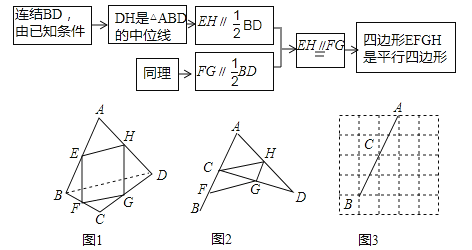
����Ŀ����ͼ1����֪��E��F��G��H�ֱ����ı���ABCD����AB��BC��CD��DA���е㣬��������˼·����֤���ı���EFGH��ƽ���ı��Σ�
��1����ͼ2����ͼ1�еĵ�C�ƶ������E�غϵ�λ�ã�F��G��H����BC��CD��DA���е㣬��֤���ı���CFGH��ƽ���ı��Σ�
��2����ͼ3���ڱ߳�Ϊ1��С��������ɵ�5��5�����У���A��C��B���ڸ���ϣ��ڸ���ϻ�����D��ʹ��C��BC��CD��DA���е�F��G��H���������CFGH��
��3���ڣ�2�����������������CFGH�ı߳���
���𰸡���1��֤������������2����ͼ����������3��![]() ��
��
��������
�����������1������BD���������ε���λ�ߵ����ʵõ�CH��BD��CH=![]() BD��ͬ��FG��BD��FG=
BD��ͬ��FG��BD��FG=![]() BD����ƽ���ı��ε��ж��������ɵõ����ۣ�
BD����ƽ���ı��ε��ж��������ɵõ����ۣ�
��2�����������ε���λ�ߵ����ʺ������ε����ʼ��ɵõ������
��3�����ݹ��ɶ����õ�BD=![]() ���������ε���λ�ߵ����ʵõ�FG=
���������ε���λ�ߵ����ʵõ�FG=![]() BD=
BD=![]() �����ǵõ����ۣ�
�����ǵõ����ۣ�
�����������1��֤������ͼ2������BD����C��H��AB��DA���е㣬��CH�ǡ�ABD����λ�ߣ���CH��BD��CH=![]() BD��ͬ��FG��BD��FG=
BD��ͬ��FG��BD��FG=![]() BD����CH��FG��CH=FG�����ı���CFGH��ƽ���ı��Σ�
BD����CH��FG��CH=FG�����ı���CFGH��ƽ���ı��Σ�
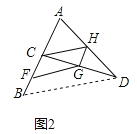
��2����ͼ3��ʾ��
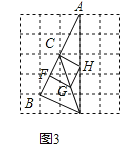
��3����ͼ3����BD=![]() ����FG=
����FG=![]() BD=
BD=![]() ����������CFGH�ı߳���
����������CFGH�ı߳���![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У���1=��2��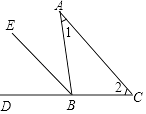
��1����������һ����ֱ��AC�йص��������ɴ˿ɵó�BE�ǡ�ABC�����ƽ���ߣ�
��2����������һ�����1�йص��������ɴ˿ɵó�BE�ǡ�ABC�����ƽ���ߣ�
��3���������֪�ڡ�ABC�У���1=��2���䡱������ѣ�1�������ӵ����������ý��ۻ��������õ������Ƿ��������⣬������ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���B=��C��AB=AC=12cm��BC=8cm����DΪAB���е㣮�����P���߶�BC����2cm/s���ٶ���B����C���˶���ͬʱ����Q���߶�CA���ɵ�C��A���˶��� 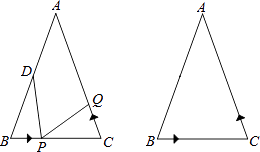
��1������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y=kx��k>0���뷴��������y= ![]() ��ͼ��ֱ���A��C���㣬��֪��B���D��������ԭ��O�����ĶԳƣ��ҵ�B������Ϊ��m �� 0��������m>0��
��ͼ��ֱ���A��C���㣬��֪��B���D��������ԭ��O�����ĶԳƣ��ҵ�B������Ϊ��m �� 0��������m>0��
��1���ı���ABCD���� �� (��д�ı���ABCD����״)
��2������A������Ϊ��n,3��ʱ���ı���ABCD�Ǿ��Σ���mn��ֵ��
��3����̽��������k��m�ı仯���ı���ABCD�ܲ��ܳ�Ϊ���Σ����ܣ���ֱ��д��k��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D��AC�ϣ���BD=BC=AD�����A���ڣ� �� 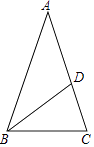
A.30��
B.40��
C.36��
D.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�㳡���������ͼ1��ʾ����ѧϰ��ֱ���������Ժ���ѧ��ȤС���������˵ĸ߶ȣ���ͼ2��ijһʱ�̣����AB��Ӱ��һ��������ƽ̨�ϣ���һ��������б���ϣ��������ƽ̨�ϵ�Ӱ��BCΪ4�ף�����б���ϵ�Ӱ��CDΪ3�ף�AB��BC��ͬһʱ�̣�������ˮƽ��ļн�Ϊ72�㣬1���������PQ��б���ϵ�Ӱ��QRΪ2�ף�����˵ĸ߶ȣ������ȷ��0.1�ף������ο����ݣ�sin72���0.95��cos72���0.31��tan72���3.08��
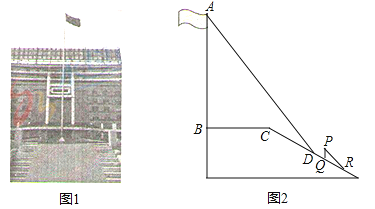
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
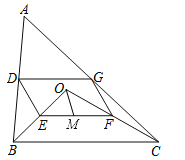
����Ŀ����ͼ����O�ǡ�ABC��һ�㣬����OB��OC������AB��OB��OC��AC���е�D��E��F��G�������ᣬ�õ��ı���DEFG��
��1����֤���ı���DEFG��ƽ���ı��Σ�
��2����MΪEF���е㣬OM=3����OBC�͡�OCB���࣬��DG�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ȵ�ʵ��m��n��������m2+3m��5��0��n2+3n��5��0����m2��n2+mn+6m��ֵΪ��������
A.14B.��14C.10D.��10
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com