
【题目】如图,已知在△ABC中,∠1=∠2.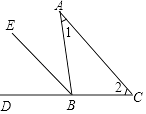
(1)请你添加一个与直线AC有关的条件,由此可得出BE是△ABC的外角平分线;
(2)请你添加一个与∠1有关的条件,由此可得出BE是△ABC的外角平分线;
(3)如果“已知在△ABC中,∠1=∠2不变”,请你把(1)中添加的条件与所得结论互换,所得的命题是否是真命题,理由是什么?
【答案】
(1)解:AC∥BE;
(2)解:∠1=∠ABE或∠1=∠DBE
(3)解:是真命题,理由如下:
∵BE是△ABC的外角平分线,
∴∠ABE=∠DBE,
又∵∠ABD是三角形ABC的外角,
∴∠ABD=∠1+∠2,
即∠ABE+∠DBE=∠1+∠2,
又∵∠ABE=∠DBE,∠1=∠2,
∴∠ABE=∠1,
∴AC∥BE.
【解析】①②要使BE是△ABC的外角平分线,结合三角形的外角的性质∠ABD=∠1+∠2,∠ABE=∠DBE,∠1=∠2,即证明∠ABE=∠1=∠DBE=∠2,进一步可得BE∥AC;
③根据平行线的性质和三角形的外角的性质即可证明。
本题综合运用了角平分线定义、平行线的性质和三角形的外角的性质。
【考点精析】本题主要考查了命题与定理的相关知识点,需要掌握我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理才能正确解答此题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
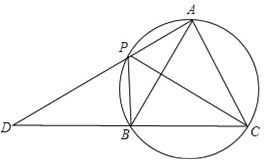
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从概率统计的角度解读下列诗词所描述的事件,其中可能性最小的是( )
A. 黄梅时节家家雨,青草池塘处处蛙 B. 人间四月芳菲尽,山寺桃花始盛开
C. 一夜北风紧,开门雪尚飘 D. 水面上秤锤浮,直待黄河彻底枯
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是函数 ![]() 与函数
与函数 ![]() 在第一象限内的图象,点P是
在第一象限内的图象,点P是 ![]() 的图象上一动点,PA⊥x轴于点A , 交
的图象上一动点,PA⊥x轴于点A , 交 ![]() 的图象于点C, PB⊥y轴于点B , 交
的图象于点C, PB⊥y轴于点B , 交 ![]() 的图象于点D.
的图象于点D.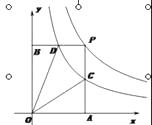
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=(x﹣4)2﹣5的顶点坐标和开口方向分别是( )
A. (4,﹣5),开口向上B. (4,﹣5),开口向下
C. (﹣4,﹣5),开口向上D. (﹣4,﹣5),开口向下
查看答案和解析>>
科目:初中数学 来源: 题型:
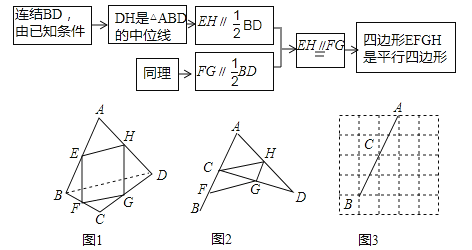
【题目】如图1,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:
(1)如图2,将图1中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;
(2)如图3,在边长为1的小正方形组成的5×5网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;
(3)在(2)条件下求出正方形CFGH的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com