
【题目】如图是函数 ![]() 与函数
与函数 ![]() 在第一象限内的图象,点P是
在第一象限内的图象,点P是 ![]() 的图象上一动点,PA⊥x轴于点A , 交
的图象上一动点,PA⊥x轴于点A , 交 ![]() 的图象于点C, PB⊥y轴于点B , 交
的图象于点C, PB⊥y轴于点B , 交 ![]() 的图象于点D.
的图象于点D.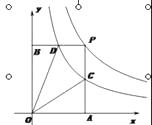
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
【答案】
(1)
证明:因为点P(x,y)在反比例函数![]() ,则可设P(x,
,则可设P(x,![]() ).则BP=x.
).则BP=x.
∵PB⊥y轴,
∴点D的纵坐标与点P的纵坐标相等,则D的纵坐标是![]() ,
,
又∵点D在反比例函数![]() ,
,
∴D(![]() ,
,![]() ),
),
则BD=![]() ,
,
BD=![]() BP,
BP,
即D是BP的中点.
(2)
解:S四边形ODPC=S四边形OAPB-S△OBD-S△OAC=6-![]() -
-![]() =3.
=3.
【解析】(1)点P与点D的纵坐标相等,可设点P(x,![]() ),再求出点D的坐标,比较横坐标.
),再求出点D的坐标,比较横坐标.
(2)利用反比例函数的系数k的几何意义做.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠1=∠2.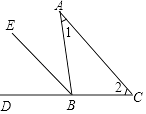
(1)请你添加一个与直线AC有关的条件,由此可得出BE是△ABC的外角平分线;
(2)请你添加一个与∠1有关的条件,由此可得出BE是△ABC的外角平分线;
(3)如果“已知在△ABC中,∠1=∠2不变”,请你把(1)中添加的条件与所得结论互换,所得的命题是否是真命题,理由是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)简便计算: ![]()
(2)计算:2a3b2(﹣3bc2)3÷(﹣ca2)
(3)先化简再求值:[(3x+2y)(3x﹣2y)﹣(x+2y)(5x﹣2y)]÷4x,其中x= ![]() ,y=2.
,y=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=∠C,AB=AC=12cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CA上由点C向A点运动. 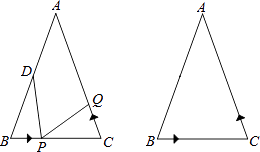
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等?请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
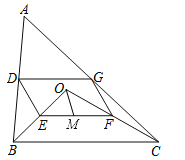
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com