
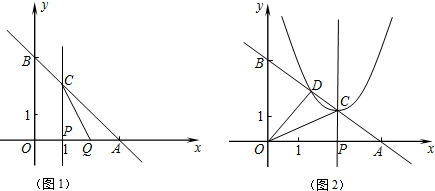
分析 (1)①根据直线方程求得A点的坐标,从而求得OA的长度;然后根据点P、Q两点的运动距离即可求得点C、Q的横坐标;将点C的横坐标代入直线方程即可求得点C的纵坐标;
②需要分类讨论:①当△AQC∽△AOB时,点P与点Q重合,OQ=OP;②当△ACQ∽△AOB时,△AOB、△ACQ都是等腰直角三角形,AQ=2CP.
(2)①以点C为顶点的抛物线,解得关于t的根,过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°,再由△DEC∽△AOB,从而解得.
②先求得三角形COD的面积为定值,又由Rt△PCO∽Rt△OAB,在线段比例中t为$\frac{36}{25}$时,h最大.
解答 解:(1)①∵直线y=-x+3分别交x轴、y轴于A,B两点,
∴令y=0,则x=3,即A(3,0).
∴OA=3;
∵点P运动1秒钟,
∴OP=1,
∵点C在直线AB上,
∴yc=-1+3=2,
∴C(1,2),
∵点Q运动时间是1秒钟,且在x轴上,
∴AQ=1,
∴OQ=OA-AQ=2,
∴Q(2,0).
综上所述,C(1,2),Q(2,0);
②由题意得:P(t,0),C(t,-t+3),Q(3-t,0).
分两种情况讨论:
情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°,
∴CQ⊥OA,
∵CP⊥OA,
∴点P与点Q重合,OQ=OP,
即3-t=t,
∴t=1.5;
情形二:当△ACQ∽△AOB时,∠ACQ=∠AOB=90°,
∵OA=OB=3,
∴△AOB是等腰直角三角形,
∴△ACQ也是等腰直角三角形.
∵CP⊥OA,
∴AQ=2CP,
即t=2(-t+3),
∴t=2.
∴满足条件的t的值是1.5秒或2秒;
(2)①由题意得:C(t,-$\frac{3}{4}$t+3),
∴以C为顶点的抛物线解析式是y=(x-t)2-$\frac{3}{4}$t+3,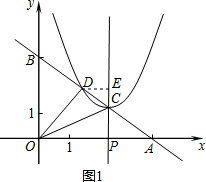
由(x-t)2-$\frac{3}{4}$t+3=-$\frac{3}{4}$x+3,
即(x-t)2+$\frac{3}{4}$(x-t)=0,
∴(x-t)(x-t+$\frac{3}{4}$)=0,
解得x1=t,x2=t-$\frac{3}{4}$.
如图1,过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°,
∵DE∥OA,
∴∠EDC=∠OAB,
∴△DEC∽△AOB,
∴$\frac{DE}{AO}$=$\frac{CD}{BA}$,
∵AO=4,AB=5,DE=t-(t-$\frac{3}{4}$)=$\frac{3}{4}$,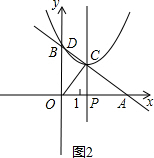
∴CD=$\frac{DE×AB}{AO}$=$\frac{\frac{3}{4}×5}{4}$=$\frac{15}{16}$,
②∵DC=$\frac{15}{16}$,CD边上的高=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴S△COD=$\frac{1}{2}$×$\frac{15}{16}$×$\frac{12}{5}$=$\frac{9}{8}$,
∴S△COD为定值.
如图2,要使OC边上的高h的值最大,只要OC最短,因为当OC⊥AB时OC最短,
此时OC的长为$\frac{12}{5}$,∠BCO=90°,
∵∠AOB=90°,
∴∠COP=90°-∠BOC=∠OBA,
又∵CP⊥OA,
∴Rt△PCO∽Rt△OAB,
∴$\frac{OP}{BO}$=$\frac{OC}{AB}$,OP=$\frac{OC×BO}{AB}$=$\frac{\frac{12}{5}×3}{5}$=$\frac{36}{25}$,
即t=$\frac{36}{25}$,
故当t为$\frac{36}{25}$秒时,h的值最大.
点评 本题考查了二次函数的综合题,以及相似三角形的判定与性质、等腰直角三角形的性质等知识,解答题时,注意要分类讨论,以防漏解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:解答题
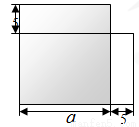
如图所示,有一个狡猾的地主,把一块边长为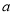 米的正方形土地租给赵老汉栽种.过了一年,他对赵老汉说:“我把你这块地的一边减少5米,另一边增加5米,继续租给你,租金不变,你也没吃亏,你看如何?”赵老汉一听,觉得好像没吃亏,就答应了. 同学们,你们觉得赵老汉有没有吃亏?请说明理由.
米的正方形土地租给赵老汉栽种.过了一年,他对赵老汉说:“我把你这块地的一边减少5米,另一边增加5米,继续租给你,租金不变,你也没吃亏,你看如何?”赵老汉一听,觉得好像没吃亏,就答应了. 同学们,你们觉得赵老汉有没有吃亏?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
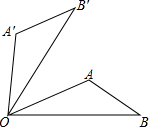 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=25°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=25°,则∠AOB′的度数是( )| A. | 60° | B. | 45° | C. | 35° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-4)^{2}}$=4 | B. | $\root{3}{(-6)^{3}}$=-6 | C. | $\sqrt{(196)^{2}}$=196 | D. | (-$\sqrt{9}$)2=-9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com