
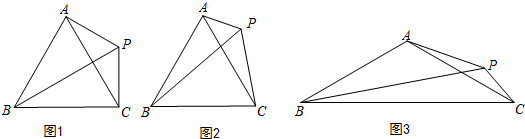
分析 (1)AB=AC,∠BAC=60°,证得△ABC是等边三角形,∠APB=∠ABC,得到∠APB=60°,又点P恰巧在∠ABC的平分线上,得到∠ABP=30°,得到直角三角形,利用直角三角形的性质解出结果.
(2)在BP上截取PD,使PD=PA,连结AD,得到△ADP是等边三角形,再通过三角形全等证得结论.
(3)以A为圆心,以AP的长为半径画弧交BP于D,连接AD,过点A作AF⊥BP交BP于F,得到等腰三角形,然后通过三角形全等证得结论.
解答 解:(1)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,∠APB=∠ABC,
∴∠APB=60°,
又∵点P恰巧在∠ABC的平分线上,
∴∠ABP=30°,
∴∠PAB=90°,
∴BP=2AP,
∵AP=2,
∴BP=4;
(2)结论:PA+PC=PB.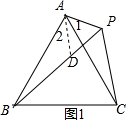
证明:如图1,在BP上截取PD,使PD=PA,连结AD,
∵∠APB=60°,
∴△ADP是等边三角形,
∴∠DAP=60°,
∴∠1=∠2,PA=PD,
在△ABD与△ACP中,
$\left\{\begin{array}{l}{PA=PD}\\{∠1=∠2}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACP,
∴PA=AD,
∴PA+PC=PB;
(3)结论:$\sqrt{3}$PA+PC=PB.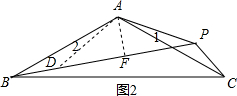
证明:如图2,以A为圆心,以AP的长为半径画弧交BP于D,连接AD,过点A作AF⊥BP交BP于F,
∴AP=AD,
∵∠BAC=120°,
∴∠ABC=30°,
∴∠APB=30°,
∴∠DAP=120°,
∴∠1=∠2,
在△ABD与△ACP中,
$\left\{\begin{array}{l}{AB=AC}\\{∠2=∠1}\\{AD=AP}\end{array}\right.$,
∴△ABD≌△ACP,
∴DB=PC,
∵AF⊥PD,
∴PF=$\frac{\sqrt{3}}{2}$AP,
∴PD=$\sqrt{3}$AP,
∴$\sqrt{3}$PA+PC=PB.
点评 本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,直角三角形的性质,等边三角形的判定和性质,作辅助线构造全等三角形是解题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
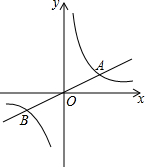 如图,已知直线y1=$\frac{1}{2}$x与双曲线y2=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.
如图,已知直线y1=$\frac{1}{2}$x与双曲线y2=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
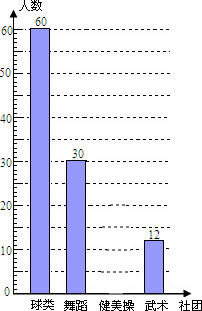 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数比例 |
| 球类 | 60 | m |
| 舞蹈 | 30 | 0.25 |
| 健美操 | n | 0.15 |
| 武术 | 12 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(天) | 1 | 2 | 3 | … | 60 |
| p(件) | 198 | 196 | 194 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
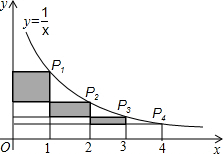 在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.
在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
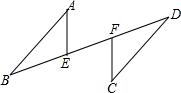 如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).
如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com