
 如图,抛物线y=-$\frac{1}{3}{x}^{2}$+2x与x轴相交于点B、O,点A是抛物线的顶点,连接AB,把AB所在的直线平移,使它经过原点O,得到直线l.已知点P是直线l上的一点,且它在x轴的上方.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t.当12≤S≤18时,t的取值范围是-3≤t≤-1.
如图,抛物线y=-$\frac{1}{3}{x}^{2}$+2x与x轴相交于点B、O,点A是抛物线的顶点,连接AB,把AB所在的直线平移,使它经过原点O,得到直线l.已知点P是直线l上的一点,且它在x轴的上方.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t.当12≤S≤18时,t的取值范围是-3≤t≤-1. 分析 如图所示:连接OA.令y=0得:-$\frac{1}{3}{x}^{2}$+2x=0,从而可求得点B的坐标为(6,0),由抛物线的对称性可知点A的横坐标为3,将x=3代入可求得点A的坐标为(3,3).利用待定系数法求得直线AB的解析式为y=-x+3,从而得到直线OP的解析式为y=-x,依据各点的坐标求得OP=-$\sqrt{2}t$,AB=3$\sqrt{2}$,OA=3$\sqrt{2}$,最后依据四边形的面积的取值范围列不等式组求解即可
解答 解:如图所示:连接OA.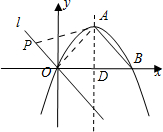
令y=0得:-$\frac{1}{3}{x}^{2}$+2x=0,
解得:x1=0,x2=6.
∴点B的坐标为(6,0).
∴点A的横坐标为3.
将x=3代入得:y=3.
∴点A的坐标为(3,3).
设直线AB的解析式为y=kx+b,将点A、B的坐标代入直线的解析式得:$\left\{\begin{array}{l}{3k+b=3}\\{6k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$.
∵直线OP∥AB,
∴直线OP的解析式为y=-x.
∵DA=DO=DB,
∴∠OAB=90°.
∵运动时间为t,
∴OP=$\sqrt{2}$t.
∴SABOP=$\frac{1}{2}(PO+AB)OA$,即12≤$\frac{1}{2}×(-\sqrt{2}t+3\sqrt{2})×3\sqrt{2}$≤18.
解得:-3≤t≤-1.
故答案为:-3≤t≤-1.
点评 本题主要考查的是抛物线与x轴的交点,根据题意列出关于四边形面积的不等式组是解题的关键.


科目:初中数学 来源: 题型:填空题
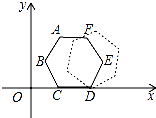 如图,平面直角坐标系中有一个正六边形ABCDEF,其中C.D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A,B,C,D,E,F中,会过点(2015,2)的是点D.
如图,平面直角坐标系中有一个正六边形ABCDEF,其中C.D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A,B,C,D,E,F中,会过点(2015,2)的是点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×108 | B. | 12×10-8 | C. | 1.2×10-8 | D. | 1.2×10-9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
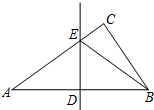 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{6}{7}$<$\frac{5}{6}$ | B. | -|-5|>-4 | C. | -$\frac{5}{6}$<-$\frac{4}{5}$ | D. | -$\frac{5}{4}$>-1.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com