
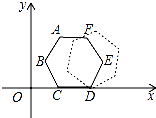
 如图,平面直角坐标系中有一个正六边形ABCDEF,其中C.D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A,B,C,D,E,F中,会过点(2015,2)的是点D.
如图,平面直角坐标系中有一个正六边形ABCDEF,其中C.D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A,B,C,D,E,F中,会过点(2015,2)的是点D. 分析 先连接A′D,过点F′,E′作F′G⊥A′D,E′H⊥A′D,由正六边形的性质得出A′的坐标,再根据每6个单位长度正好等于正六边形滚动一周即可得出结论.
解答 解:如图所示: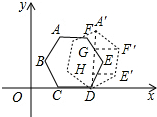
当滚动到A′D⊥x轴时,E、F、A的对应点分别是E′、F′、A′,
连接A′D,点F′,E′作F′G⊥A′D,E′H⊥A′D,
∵六边形ABCDEF是正六边形,
∴∠A′F′G=30°,
∴A′G=$\frac{1}{2}$A′F′=$\frac{1}{2}$,同理可得HD=$\frac{1}{2}$,
∴A′D=2,
∵D(2,0)
∴A′(2,2),OD=2,
∵正六边形滚动6个单位长度时正好滚动一周,
∴从点(2,2)开始到点(2015,2)正好滚动2013个单位长度,
∵$\frac{2013}{6}$=335…3,
∴恰好滚动335周多3个,
∴会过点(2015,2)的是点D.
故答案为:D.
点评 本题考查的是正多边形和圆及图形旋转的性质;根据题意作出辅助线,利用正六边形的性质求出A′点的坐标是解答此题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
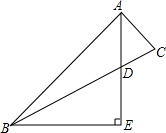 已知:如图,在△ABC中,AB=3AC,AD平分∠BAC,BE⊥AD交AD的延长线于点E.设△ACD的面积是S.
已知:如图,在△ABC中,AB=3AC,AD平分∠BAC,BE⊥AD交AD的延长线于点E.设△ACD的面积是S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,抛物线y=-$\frac{1}{3}{x}^{2}$+2x与x轴相交于点B、O,点A是抛物线的顶点,连接AB,把AB所在的直线平移,使它经过原点O,得到直线l.已知点P是直线l上的一点,且它在x轴的上方.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t.当12≤S≤18时,t的取值范围是-3≤t≤-1.
如图,抛物线y=-$\frac{1}{3}{x}^{2}$+2x与x轴相交于点B、O,点A是抛物线的顶点,连接AB,把AB所在的直线平移,使它经过原点O,得到直线l.已知点P是直线l上的一点,且它在x轴的上方.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t.当12≤S≤18时,t的取值范围是-3≤t≤-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com