
���� ��1�����������ε����ʺ�ȫ�������ε��ж�����֤��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����ȫ�������ε����ʼ��������EAF=$\frac{1}{2}$��BAD=45�㣻
��2���ɣ�1��֪��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF����AG=x����CE=x-2��CF=x-3����ΪCE2+CF2=EF2�����ԣ�x-2��2+��x-3��2=52����������̣����x��ֵ���ɵõ�AG=6���ڣ�2���У�MN2=MB2+ND2��MN=a��${a}^{2}=��3/2\sqrt{2}��^{2}+��6\sqrt{2}-3/2\sqrt{2}-a��^{2}$������a=$\frac{5\sqrt{2}}{2}$����MN=$\frac{5\sqrt{2}}{2}$��
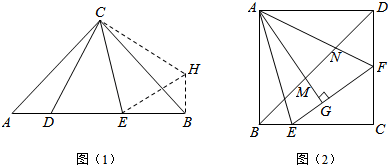
��� �⣺���ݡ��߽DZߡ�����֤��CEH�ա�CDE����EH=ED��
��Rt��HBE�У��ɹ��ɶ������ɵ�BH2+EB2=EH2����BH=AD���ɵ�AD��DE��EB֮��ĵ�����ϵ��AD2+EB2=DE2���ʴ�Ϊ����CDE�����ɣ�AD2+EB2=DE2��
��1����Rt��ABE��Rt��AGE��
$\left\{\begin{array}{l}{AB=AG}\\{AE=AE}\end{array}\right.$��
��Rt��ABE��Rt��AGE��HL����
���BAE=��GAE��
ͬ����Rt��ADF��Rt��AGF��
���GAF=��DAF��
���ı���ABCD�������Σ�
���BAD=90�㣬
���EAF=$\frac{1}{2}$��BAD=45�㣻
��2���ɣ�1��֪��Rt��ABE��Rt��AGE��Rt��ADF��Rt��AGF��
��BE=EG=2��DF=FG=3����EF=5��
��AG=x����CE=x-2��CF=x-3��
��CE2+CF2=EF2��
�ࣨx-2��2+��x-3��2=52��
��������̣���x1=6��x2=-1����ȥ����
��AG=6��
��BD=$\sqrt{A{B}^{2}+A{D}^{2}}=\sqrt{2A{G}^{2}}=6\sqrt{2}$��
��AB=6��
��MN2=MB2+ND2
��MN=a����${a}^{2}=��3/2\sqrt{2}��^{2}+��6\sqrt{2}-3/2\sqrt{2}-a��^{2}$��
����a=$\frac{5\sqrt{2}}{2}$��
��MN=$\frac{5\sqrt{2}}{2}$��
���� ���⿼���������ε����ʡ�ֱ�������ε����ʡ�ȫ�������ε��ж��������Լ����ɶ��������ú�һԪ���η��̵����ã���Ŀ���ۺ��Ժ�ǿ���ѶȲ�С��


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
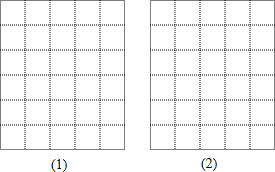 ��ͼ�������������е�ÿ��С�����α߳���Ϊ1��ÿ��С�����εĶ���и�㣬�Ը��Ϊ����ֱ�����Ҫ�������κ�ƽ���ı��Σ�
��ͼ�������������е�ÿ��С�����α߳���Ϊ1��ÿ��С�����εĶ���и�㣬�Ը��Ϊ����ֱ�����Ҫ�������κ�ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����C��D���߶�AB�ϣ��ҡ�PCD�ǵȱ������Σ�
��ͼ����C��D���߶�AB�ϣ��ҡ�PCD�ǵȱ������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
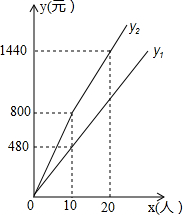 �̽��캣̲������Ʊ�۸�80Ԫ/�ˣ�����Ϊ�����οͣ�����Ʊ�۸���ж�̬�������ǽڼ��մ�a�ۣ��ڼ����ڼ䣬10�����£�����10�ˣ������ۣ�10�����ϳ���10�˵IJ��ִ�b�ۣ����ο�Ϊx�ˣ���Ʊ����ΪyԪ���ǽڼ�����Ʊ����y1��Ԫ�����ڼ�����Ʊ����y2��Ԫ�����ο�x���ˣ�֮��ĺ�����ϵ��ͼ��ʾ��
�̽��캣̲������Ʊ�۸�80Ԫ/�ˣ�����Ϊ�����οͣ�����Ʊ�۸���ж�̬�������ǽڼ��մ�a�ۣ��ڼ����ڼ䣬10�����£�����10�ˣ������ۣ�10�����ϳ���10�˵IJ��ִ�b�ۣ����ο�Ϊx�ˣ���Ʊ����ΪyԪ���ǽڼ�����Ʊ����y1��Ԫ�����ڼ�����Ʊ����y2��Ԫ�����ο�x���ˣ�֮��ĺ�����ϵ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com