
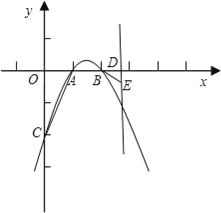
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

【答案】(1)二次函数的解析式为y=﹣x2+3x﹣2;
(2)E点坐标为E1(m, ![]() ),E2(m,4﹣2m);
),E2(m,4﹣2m);
(3)F点的坐标为:F1(![]() ,﹣
,﹣![]() ),F2(4,﹣6).
),F2(4,﹣6).
【解析】试题分析:
(1)已知抛物线经过三个点,则可设抛物线的解析式为一般式![]() ,再将三个点的坐标代入到一般式中,得到三元一次方程组即可求解;
,再将三个点的坐标代入到一般式中,得到三元一次方程组即可求解;
(2)△AOC与△BDE都是直角三角形,除直角外,其它的对应关系不确定,所以应分两类讨论,由相似三角形的对应边成比例求出E点的坐标;
(3)A,B是两个确定的点,E点的坐标中含有m也可看作是确定的点,则可根据三个点的坐标,确定第四个点F的坐标,而点F在抛物线上,把F点的坐标代入到抛物线中得到关于m的方程,则可求出点F的坐标.
解:(1)将点A(1,0),B(2,0),C(0,﹣2)代入二次函数y=ax2+bx+c中,得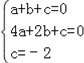
解得a=﹣1,b=3,c=﹣2.
∴y=﹣x2+3x﹣2.(2分)
(2)∵AO=1,CO=2,BD=m﹣2,
当△EDB∽△AOC时,得![]() =
=![]() ,
,
即![]() =
=![]() ,解得ED=
,解得ED=![]() ,
,
∵点E在第四象限,
∴E1(m,![]() ),
),
当△BDE∽△AOC时,![]() =
=![]() 时,即
时,即![]() =
=![]() ,
,
解得ED=2m﹣4,
∵点E在第四象限,
∴E2(m,4﹣2m);
所以有E1(m,![]() ),E2(m,4﹣2m).
),E2(m,4﹣2m).
(3)假设抛物线上存在一点F,使得四边形ABEF为平行四边形,则
EF=AB=1,点F的横坐标为m﹣1,
当点E1的坐标为(m,![]() )时,点F1的坐标为(m﹣1,
)时,点F1的坐标为(m﹣1,![]() ),
),
∵点F1在抛物线的图象上,
∴![]() =﹣(m﹣1)2+3(m﹣1)﹣2,
=﹣(m﹣1)2+3(m﹣1)﹣2,
∴2m2﹣11m+14=0,
∴(2m﹣7)(m﹣2)=0,
∴m=![]() ,m=2(舍去),
,m=2(舍去),
∴F1(![]() ,﹣
,﹣![]() ),
),
当点E2的坐标为(m,4﹣2m)时,点F2的坐标为(m﹣1,4﹣2m),
∵点F2在抛物线的图象上,
∴4﹣2m=﹣(m﹣1)2+3(m﹣1)﹣2,
∴m2﹣7m+10=0,
∴(m﹣2)(m﹣5)=0,∴m=2(舍去),m=5,
∴F2(4,﹣6).
所以F1(![]() ,﹣
,﹣![]() ),F2(4,﹣6).
),F2(4,﹣6).


科目:初中数学 来源: 题型:
【题目】一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
(1)写出第一次移动后这个点在数轴上表示的数为 ;
(2)写出第二次移动后这个点在数轴上表示的数为 ;
(3)写出第五次移动后这个点在数轴上表示的数为 ;
(4)写出第![]() 次移动结果这个点在数轴上表示的数为 ;
次移动结果这个点在数轴上表示的数为 ;
(5)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和
(﹣2,0)之间,其部分图象如下图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
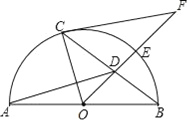
【题目】如图,AB是半圆O上的直径,E是![]() 的中点,OE交弦BC于点D,过点C作⊙O的切线交OE的延长线于点F,已知BC=8,DE=2.
的中点,OE交弦BC于点D,过点C作⊙O的切线交OE的延长线于点F,已知BC=8,DE=2.
(1)求⊙O的半径;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在网购已成为人们的一种消费方式,在2015年的“双11”促销活动中天猫和淘宝的支付交易额突破57000000000元,将数字57000000000用科学记数法表示为元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(﹣3,4)关于y轴的对称点为点B,连接AB,反比例函数y= ![]() (x>0)的图像经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图像上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(x>0)的图像经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图像上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ. 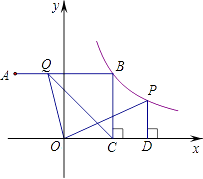
(1)点B的坐标是;k的值为
(2)判断△QDC与△POD的面积是否相等,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com