
����Ŀ�������� x ��һԪ���η���axbxc=0��a0��c0��a��b��cΪ����������������ȵ�ʵ����![]() ��
��![]() ��0
��0![]()
![]() ����OΪ����ԭ�㣬A��BΪx���������ϵ�������A
����OΪ����ԭ�㣬A��BΪx���������ϵ�������A![]() ��0��B
��0��B![]() ��0.
��0.
��1����![]() =c=2,b=-
=c=2,b=-![]() ʱ����
ʱ����![]() ��a��ֵ;
��a��ֵ;
��2���� x 1��c 6a ʱ��PΪһ�κ��� y x4ͼ����һ�㣬QΪƽ��ֱ������ϵ�е�һ�㣬���� A��B��P��Q Ϊһ�����ε��ĸ����㣬��ȷ����Q�����ꣻ
��3����![]() =2cʱ������������������y=
=2cʱ������������������y=![]() ��ͼ�����Ƿ���ڵ�Mʹ����ABMΪ�ȱ������Σ��жϲ�֤����Ľ��ۡ�
��ͼ�����Ƿ���ڵ�Mʹ����ABMΪ�ȱ������Σ��жϲ�֤����Ľ��ۡ�

���𰸡���1��![]() =3��a=
=3��a=![]() ����2����Q������Ϊ����6��3����1��-2������3�������ڵ�Mʹ����ABMΪ�ȱ������Σ�֤��������.
����2����Q������Ϊ����6��3����1��-2������3�������ڵ�Mʹ����ABMΪ�ȱ������Σ�֤��������.
��������
��1����![]() =c=2��b=
=c=2��b=![]() ��������a��ֵ���Ӷ��õ��÷��̣����ø���ϵ���Ĺ�ϵ�������һ����
��������a��ֵ���Ӷ��õ��÷��̣����ø���ϵ���Ĺ�ϵ�������һ����
��2����x1��c6a��������b=-7a���Ӷ������̱���Ϊa(x-1)(x-6)=0���õ�A��B���꣬Ȼ�����һ�κ���ͼ���ϵ�����������;��ε����ʿɷ���������Q�����ꣻ
��3����![]() =2c����axbx c=0���ø���ϵ���Ĺ�ϵ���
=2c����axbx c=0���ø���ϵ���Ĺ�ϵ���![]() ���õ�A��B���꣬����M��MC��x���ڵ�C����C��AB�е㣬�����C�����꣬����������������������ʽ�õ�M�����꣬Ȼ�����CM=
���õ�A��B���꣬����M��MC��x���ڵ�C����C��AB�е㣬�����C�����꣬����������������������ʽ�õ�M�����꣬Ȼ�����CM=![]() AC�г��������bֵ���Ƴ�ì�ܣ�����ý�.
AC�г��������bֵ���Ƴ�ì�ܣ�����ý�.
�⣺��1����![]() =c=2��b=
=c=2��b=![]() ����ax bx c=0�ã�4a+2��(
����ax bx c=0�ã�4a+2��(![]() )+2=0��
)+2=0��
��ã�a=![]() ��
��
���Ը÷���Ϊ��![]() x
x![]() x 2=0��
x 2=0��
��![]() =
=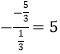 ����2+
����2+![]() =5��
=5��
��![]() =3��
=3��
��2����x1��c6a����axbx c=0��ab6a=0��
��b=-7a��
��ax-7ax 6a=0����a(xx 6)=0��
��a(x-1)(x-6)=0��a0����
��![]() ��
��![]() ��
��
��A(1��0)��B(6��0)��
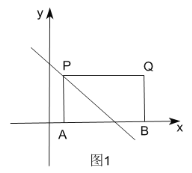
����ͼ1������A��AP��x�ύֱ��yx4�ڵ�P��
��P��1��3����
���ı���APQBΪ���Σ�
��Q��6��3����
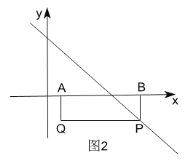
����ͼ2������B��BP��x�ύֱ��yx4�ڵ�P��
��P��6��-2����
���ı���ABPQΪ���Σ�
��Q��1��-2����
������������Q����������6��3����1��-2����
��3�������ڵ�Mʹ�á�ABMΪ�ȱ������Σ�
֤������![]() =2c����axbx c=0�ã�4ac2+2bc+c=0����c(4ac+2b+1)=0��
=2c����axbx c=0�ã�4ac2+2bc+c=0����c(4ac+2b+1)=0��
��c0��
��4ac+2b+1=0�٣�
��![]() ��
��
��![]() ��
��
��A(2c��0)��B(![]() ��0)��
��0)��
������ڵ�Mʹ�á�ABMΪ�ȱ������Σ�
��ͼ3������M��MC��x���ڵ�C����C��AB�е㣬
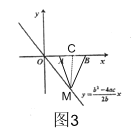
��C���������![]() ��
��
��![]() ����
����![]() �ɵ�
�ɵ�![]() ��
��
�ɢٿ�֪4ac=-(2b+1)��4ac+1=-2b��
��![]() ��
��
��M��![]() ��
��![]() ����
����
����ABMΪ�ȱ�������ʱ��CM=![]() AC��
AC��
AC![]() ��
��
��![]()
��![]() ��
��
��ã�b=-1���ᣩ��b=![]() ��
��
��b=![]() ��
��![]() ��
��
��a��0����������a0ì�ܣ�
����ڵ�Mʹ�á�ABMΪ�ȱ�������.


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�һ�����ƻ���,֣���н�����������ɫ���г�������,��֪A�ͺŵ����г���B�ͺŵ����г��ĵ��۵�30Ԫ,��8��A�ͺŵ����г�����7��B�ͺŵ����г�����������ͬ.
(1)A,B�����ͺŵ����г��ĵ��۷ֱ��Ƕ���?
(2)������A,B�������г���600��,��A�ͺ����г�������������B�ͺ����г���һ��,�������һ����ʡǮ�ķ���,������÷�������Ҫ�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��1��a���Ƿ���������![]() ��ͼ����һ�㣬ֱ��
��ͼ����һ�㣬ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ������Ľ���Ϊ��B��
��ͼ���ڵ������Ľ���Ϊ��B��
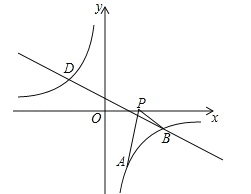
��1����ֱ��AB�Ľ���ʽ��
��2������P��x��0����x������������˶������߶�PA���߶�PB֮��ﵽ���ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
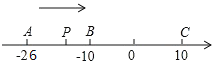
����Ŀ����֪��������A��B��C���㣬�ֱ��ʾ��������26����10��10������P��A��������ÿ��1����λ���ٶ������ƶ�����P���˶���C��ʱ�˶�ֹͣ������P�ƶ�ʱ��Ϊt����
(1)�ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺PA=_____��PC=_____��
(2)����P�˶���B��ʱ����Q��A��������ÿ��3����λ���ٶ������˶�����t���ڶ�����ʱP��Q��������?t���ڶ�����ʱP��Q�������4����λ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A,B������ͬһ�������ϣ���A��ԭ�����ߣ���ԭ��ľ���Ϊ4����B��ԭ���ұߣ���A ��B��ľ���Ϊ16.
��1����A,B��������ʾ������
��2����A,B����ֱ���ÿ��1����λ���Ⱥ�3����λ���ȵ��ٶ�ͬʱ�����ƶ����ڵ�C���������C��ʾ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��֯��Ա������³ɹ����������ѧУ�ﳵ�����������µ���A�غ�����8���ӣ�Ȼ�����µ�B������8���ӷ��أ��г������ͼ��������ʱ���ϡ������ٶ��Ա��ֲ��䣬��A����Ҫ����8���ӣ���ô���Ǵ�B�ط���ѧУ�õ�ʱ���ǣ� ��

A. 45.2���� B. 48���� C. 46���� D. 33����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ����ͼ��ʾ��
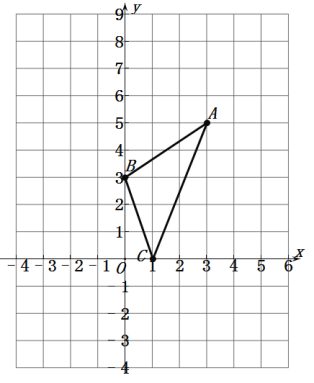
��1��S��ABC���� ��
��2��x�����Ƿ���ڵ�P��ʹ��S��BCP��2S��ABC���������ڣ�˵�����ɣ������ڣ����P������꣮
��3����ֱ��д������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ��ȤС���У�С��������ѧ̽��������߳�Ϊ2��������ABCD��߳�Ϊ3��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһ��ֱ���ϣ�AB��AG��ͬһ��ֱ���ϣ�
(1)С������DG=BE��DG��BE���������֤����
(2)��ͼ2��С����������ABCD�Ƶ�A��ʱ����ת������Bǡ�������߶�DG��ʱ��������������ʱ��ADG�������
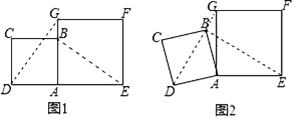
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ a b �� a ��b �������������϶�Ӧ�ĵ�ֱ�Ϊ�� A ���� B ���� A �� B ����֮��ľ���.
��̽����
С�����þ���ֵ�ĸ��������ᣬ����̽����

��1����ȫС����̽��
��Ӧ�ã�
��2������C ��Ӧ����c �������ϵ�C ��A��B ����ľ�����ȣ���c .���ú�a��b �Ĵ���ʽ��ʾ��
��3������ D��Ӧ���� d �������ϵ� D �� A �ľ����ǵ� D �� B �ľ����nn 0 ������̽�� n ��ȡֵ��Χ��� D �����Ĺ�ϵ����ֱ��д��a��b ��d��n �Ĺ�ϵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com