练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知A,B两点在同一条数轴上，点A在原点的左边，到原点的距离为4，点B在原点右边，点A 到B点的距离为16.

    （1）求A,B两点所表示的数：

    （2）若A,B两点分别以每秒1个单位长度和3个单位长度的速度同时相向移动，在点C相遇，求点C表示的数？

    【答案】（1）点A表示的数为-4，点B表示的数为12；（2）点C表示的数为0.

    【解析】

    （1）根据数轴上原点左边的数为负数，右边的数为正数，可求出A点表示的数，再根据两点间的距离公式得到B点表示的数；

    （2）设C点表示的数为c，根据相遇问题中运动时间相等，建立方程求解.

    解：（1）设A点表示的数为，由题意得，则

    又因为A在原点的左边，所以A点表示的数为

    设B点表示的数为，由AB距离16可得，即，∴或12

    又因为点B在原点右边，所以B点表示的数为12.

    （2）设C点表示的数为c，由题意得

    ，解得

    故点C表示的数为0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某玩具店将进货价为元的玩具以元的销售价售出,平均每月能售出个市场调研表明:当销售价每涨价元时,其销售量将减少2个.

    (1)设每个玩具的销售价上涨元,试用含的式子填空:

    ①涨价后,每个玩具的销售价为 元；

    ②涨价后,每个玩具的利润为 元；

    ③涨价后,玩具的月销售量为 个.

    (2)玩具店老板要想让该玩具的销售利润平均每月达到1600元,销售员甲说:“在原售价每个90元的基础上再上涨30元,可以完成任务”销售员乙说:“不用涨那么多,在原售价每个90元的基础上再上涨10元就可以了”判断销售员甲与销售员乙的说法是否正确,并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解题）先阅读下列一段文字，然后解答问题：

    已知：方程

    方程

    方程

    方程

    问题：观察上述方程及其解，再猜想出方程： 的解，并试着解分式方程验证．

    【答案】

    【解析】试题分析：首先通过观察发现，它的规律是：方程x的解为x1=n+1，x2＝，利用这个规律就可以求出方程的解．

    试题解析：∵

    ∴x2-11x-120=0

    解得： .

    【题型】解答题
    【结束】
    20

    【题目】（2017北京市）关于x的一元二次方程．

    （1）求证：方程总有两个实数根；

    （2）若方程有一根小于1，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为丰富居民业余生活，某居民区组建筹委会，该筹委会动员居民自愿集资建立一个书刊阅览室.经预算，一共需要筹资30 000元，其中一部分用于购买书桌、书架等设施，另一部分用于购买书刊.

    （1）筹委会计划，购买书刊的资金不少于购买书桌、书架等设施资金的3倍，问最多用多少资金购买书桌、书架等设施？

    （2）经初步统计，有200户居民自愿参与集资，那么平均每户需集资150元.镇政府了解情况后，赠送了一批阅览室设施和书籍，这样，只需参与户共集资20 000元.经筹委会进一步宣传，自愿参与的户数在200户的基础上增加了ａ%（其中）.则每户平均集资的资金在150元的基础上减少了%，求ａ的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列各题并按要求完成：

    （1）定义：若两个一元二次方程有一个相同的实数根，则称这两个方程为“友好方程”，已知关于x的一元二次方程 x 2x 0 与 x 3x m 1 0 为“友好方程”，求 m 的值；

    （2）关于x的一元二次方程 有两个不相等的实数根,,且二次根式有意义，若T=，求T的取值范围;

    （3）我们不妨约定方程的整数解称之为“硬核”，例如x=1就称为方程(x-1)(2x+1)=0 的一个“硬核”，若一元二次方程(k-3k+2)x+(2k-4k+1)x+k-k=0（k为常数）有两个不同的“硬核”，试确定方程的两个“硬核”及常数 k 的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若关于 x 的一元二次方程axbxc=0（a0，c0，a、b、c为常数）有两个不相等的实数根，（0），O为坐标原点，A、B为x轴正半轴上的两点且A，0，B，0.

    （1）当=c=2,b=-时，求与a的值;

    （2）当 x 1，c 6a 时，P为一次函数 y x4图象上一点，Q为平面直角坐标系中的一点，若点 A、B、P、Q 为一个矩形的四个顶点，请确定点Q的坐标；

    （3）当=2c时，试问在正比例函数y=的图象上是否存在点M使得△ABM为等边三角形？判断并证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上，梯子与地面的倾斜角α为60°．

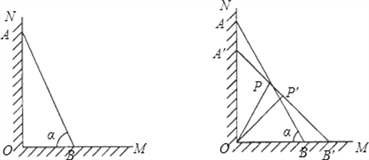
    （1）求AO与BO的长；

    （2）若梯子顶端A沿NO下滑，同时底端B沿OM向右滑行．如图（2），当A点下滑到A′点，B点向右滑行到B′点时，梯子AB的中点P也随之运动到P′点，若∠POP′=15°，试求AA′的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了这15人某月的加工零件个数．（如下表）

    每人加工零件数

    54

    45

    30

    24

    21

    12

    人 数

    1

    1

    2

    6

    3

    2

    （1）写出这15人该月加工零件数的平均数、中位数和众数；

    （2）假设生产部负责人把每位工人的月加工零件数定为24件，你认为是否合理？为什么？如果不合理，请你设计一个较为合理的生产定额，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，直线y＝－x＋1与抛物线y＝ax2＋bx＋c(a≠0)相交于点A(1，0)和点D(－4，5)，并与y轴交于点C，抛物线的对称轴为直线x＝－1，且抛物线与x轴交于另一点B.

    (1)求该抛物线的函数表达式；

    (2)若点E是直线下方抛物线上的一个动点，求出△ACE面积的最大值；

    (3)如图2，若点M是直线x＝－1的一点，点N在抛物线上，以点A，D，M，N为顶点的四边形能否成为平行四边形？若能，请直接写出点M的坐标；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案